In this post on Gambling and Expected Value, we look at the "NHL Lotto" lottery offered by the OLG.
Click here to find similar posts on other lotteries and games of chance.
Click here to find similar posts on other lotteries and games of chance.
NHL Lotto (OLG)
NHL Lotto a lottery offered by the Ontario Lottery and Gaming Corporation (OLG).
How the Game Works
To play NHL Lotto, the player selects a combination of 5 numbers chosen from 1 to 30, and an NHL team (of which there are also 30 options). Numbers cannot be repeated and the order is not important. The player also has the option of having the computer generate a random selection instead (known as "Quick Pick" in lottery vernacular). The game involves two portions, the "Instant Win" and the "Nightly Draw". In the Instant Win portion, you watch a computer-generated animation of a hockey player take three shots at a net with targets and hope that you've been randomly selected to be a winner. The system has been programmed to randomly mete out prizes based on OLGs predetermined odds of winning. In the Nightly Draw, prizes are awarded based on correctly matching the winning numbers and NHL team. It costs $2 to play NHL Lotto.
Probabilities and Prizes
There are 13 different ways to win a prize in the Instant Win portion of NHL Lotto, ranging from $15,000 down to $2. The prize awarded corresponds to the targets hit by your computer generated hockey player, but it's not clear how exactly that translates into calculable probabilities. I'll have to assume the odds reported by the OLG are the exact probabilities programmed into their computers. But here's the summary of the Instant Win prizes and probabilities for NHL Lotto:
There are 142,506 unique combinations of five numbers that can be chosen from the numbers 1 to 30. The number of combinations of items you can choose from a set without repetition is calculated using the following formula:
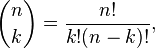
where k is the number of items chosen, n is the total number of item to choose from, and ! denotes the factorial function. In this case, n = 30 and k = 5. But you also choose one hockey team out of 30 possible choices. You could repeat the above calculation for n = 30 and k = 1, but it should be intuitively obvious that there are 30 possible ways to pick one hockey team out of the 30. So in total there are 30 times 142,506 = 4,275,180 unique combinations of one NHL team plus 5 numbers chosen from the numbers 1 to 30.
The probability of matching some number of the winning 5 can be calculated from the hypergeometric distribution. The formula looks like this:
where p is the probability of winning, n is the size of the set of numbers the winners are drawn from, k is the size of a combination, and r is the number of matching numbers required to win the prize. For example, to calculate the probability of matching four numbers in NHL Lotto, r = 4, k = 5, and n = 30. Plugging in the numbers gives the probability of approximately 0.088%, or about 1 in 1,140 (note this probability reflects the combined probability of winning either the 3rd or 4th prizes).
We can treat the NHL team matching as a bonus number drawn from a separate pool of numbers. The formula to calculate the probability of matching r out of k winning numbers plus a bonus number that is drawn from a separate pool of m numbers is a slight modification of Equation 1:
Here is a table summarizing the payouts of the Nightly Draw portion of NHL Lotto and their probabilities:
Since for some of the prizes matching x out of 5 numbers has two different prizes depending on whether or not you match the NHL team, the probability has to be adjusted for overcounting. The probability of matching with the bonus is calculated from Equation 2 (m = 30). The probability of matching without the bonus is calculated from Equation 1 minus Equation 2.
So there's roughly 66.7% chance you lose on the Instant Win game and 94.5% you lose on the Nightly Draw. The combined probability of losing both games is calculated by multiplying the two probabilities together, which works out to a 63.1% probability that an NHL Lotto player has just thrown his money away.
 |
| Summary of prizes and their probabilities in the Instant Win portion of NHL Lotto |
There are 142,506 unique combinations of five numbers that can be chosen from the numbers 1 to 30. The number of combinations of items you can choose from a set without repetition is calculated using the following formula:
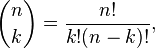
The probability of matching some number of the winning 5 can be calculated from the hypergeometric distribution. The formula looks like this:
 |
| Equation 1 (general lottery prize probability formula) |
where p is the probability of winning, n is the size of the set of numbers the winners are drawn from, k is the size of a combination, and r is the number of matching numbers required to win the prize. For example, to calculate the probability of matching four numbers in NHL Lotto, r = 4, k = 5, and n = 30. Plugging in the numbers gives the probability of approximately 0.088%, or about 1 in 1,140 (note this probability reflects the combined probability of winning either the 3rd or 4th prizes).
We can treat the NHL team matching as a bonus number drawn from a separate pool of numbers. The formula to calculate the probability of matching r out of k winning numbers plus a bonus number that is drawn from a separate pool of m numbers is a slight modification of Equation 1:
 |
| Equation 2 (general lottery with separate bonus number prize probability formula) |
Here is a table summarizing the payouts of the Nightly Draw portion of NHL Lotto and their probabilities:
 |
| Summary of prizes and their probabilities for the Nightly Draw portion of NHL Lotto. |
So there's roughly 66.7% chance you lose on the Instant Win game and 94.5% you lose on the Nightly Draw. The combined probability of losing both games is calculated by multiplying the two probabilities together, which works out to a 63.1% probability that an NHL Lotto player has just thrown his money away.
Expected Value
Expected value here is pretty straightforward to calculate, just multiply each of the possible prizes by its respective probability, sum all the products, and then subtract the cost of the ticket. For example, the $100,000 prize in the Nightly Draw multiplied by the 1/4,275,180 probability of winning contributes an expected value of $100,000/4,275,180 (about 2.34 cents) to the overall expected value of an NHL Lotto ticket.
From the tables, you can see there's a house edge of about 41.3%, meaning an average of 41.3 cents from every dollar spent on NHL Lotto goes straight to the OLG.
It's interesting to compare the two games. The total expected value of the Instant Win prizes is more than 4 times the expected value of Nightly Draw prizes. Similarly, the probability of getting a payout in the Instant Win portion is about 6 times the probability of getting a payout in the Nightly Draw. The OLG cleverly use a little computer animation, which is probably slightly entertaining to watch, and the fact that you get a payout about a third of the time, to hook people on the game. Most people appreciate that the chance of winning exists only if they buy a ticket, but don't really appreciate how minuscule that chance might be. The Nightly Draw is there to give players hope. The thinking is that if you lose the Instant Win game, well at least you've got another shot at free money. Too bad your chance of winning anything in the Nightly Draw is much lower than in the Instant Win. The Nightly Draw is even assigned a bigger top prize, because when the payout gets bigger, people tend to be more willing to make bad decisions (like buying another ticket).
From our analysis we can draw the following conclusions:
 |
| Summary of expected values of the prizes in the Instant Win portion of NHL Lotto |
 |
| Summary of expected values of the prizes in the Nightly Draw portion of NHL Lotto with overall expected value and house edge of NHL Lotto |
It's interesting to compare the two games. The total expected value of the Instant Win prizes is more than 4 times the expected value of Nightly Draw prizes. Similarly, the probability of getting a payout in the Instant Win portion is about 6 times the probability of getting a payout in the Nightly Draw. The OLG cleverly use a little computer animation, which is probably slightly entertaining to watch, and the fact that you get a payout about a third of the time, to hook people on the game. Most people appreciate that the chance of winning exists only if they buy a ticket, but don't really appreciate how minuscule that chance might be. The Nightly Draw is there to give players hope. The thinking is that if you lose the Instant Win game, well at least you've got another shot at free money. Too bad your chance of winning anything in the Nightly Draw is much lower than in the Instant Win. The Nightly Draw is even assigned a bigger top prize, because when the payout gets bigger, people tend to be more willing to make bad decisions (like buying another ticket).
From our analysis we can draw the following conclusions:
- NHL Lotto has a house edge of about 41.3%, which is a little better than a 50/50 draw. In other words, on average, OLG keeps 41.3 cents of every dollar spent playing NHL Lotto. Better than a lot of lotteries, but worse than casino games.
- The Instant Win portion of the game is significantly better than the Nightly Draw portion, both in terms of the expected prize value (about 4 times that of the Nightly Draw), and the odds of winning a payout (about 6 times higher chance of winning than in the Nightly Draw).
- The combination of flashy animation, small and relatively frequent payouts, and a second chance game that has a bigger top prize (but rarely pays out to anyone) is purposefully crafted to attract and hook gamblers on NHL Lotto.
Very interesting and in-depth analysis, thanks for sharing it with us. It gives rather broad picture. I'll try to do the same for Thunderball.
ReplyDeleteHello viewers around the Globe, I was despondent because i had a very small penis, about 2.5 inches soft and 4 inches hard not nice enough to satisfy a woman, i have been in so many relationship, but cut off because of my situation, i have used so many product which doctors for me, but none could offer me the help i searched for. i saw some few comments on the INTERNET about this specialist called Dr,OLU and decided to contact him on his email: Drolusolutinthome@gmail.com) so I decided to give his herbal product a try. i emailed him and he got back to me, he gave me some comforting words with his herbal pills for Penis Enlargement, Within 3 week of it, i began to feel the enlargement was surprised when she said that she is satisfied with my sex and i have got a large penis. Am so happy, thanks to Dr OLU I also learn that Dr OLU also help with Breast Enlargement Hips and Bums Enlargement etc.. If you are in any situation with a little Penis, weak ejaculation, small breast_hips_bums do get to Dr OLU now for help on his email (Drolusolutionhome@gmail.com) or add him on whatsapp line +2348140654426
DeleteHi Guys….I just want to say a big thanks to ( Dr Ogbe ) for what he has done for me and my family by helping me to win lottery. I won Five Hundred and Thirty Three Million Us Dollars. (($533,000,000.00)). His lottery spell is the best and so amazing. My life is now balance and i am Now Very Rich As i have always wanted and i am out of doubt. Are you looking for a real and genuine spell caster to help you win big in any kind of lottery you play? you can contact DrOgbe , today all your plan to ever win Big in Lottery will Come True and work out well for you. His spell very real and genuine i can not still believe it And His spell also work very fast. Thank you so much Dr Ogbe for dedicating your time to cast the Lottery spell for me. I got my bills paid and my debt cleared and am still mega rich. If you need a real And Genuine spell caster to help you Win lottery,kindly contact him for fast and urgent Help Email: drogbeherbalcure5@gmail.com whatsapp numbers +2347063915230THANK YOU FOR READING
DeleteCONTACT THE BEST LOTTERY SPELL CASTER FOR THE RIGHT LOTTERY NUMBERS NOW HIS LOTTERY SPELL IS 100% GUARANTEE WHATSAPP +2348118829899
DeleteHello everyone am Raymond from Pennsylvania USA I want to share my wonderful testimony of how a powerful spell caster called Dr Great helped me to win lottery, i have been playing lottery for a long time now but I had no luck everything changed when I messaged Dr Great about winning the lottery he assured me that I will be the next winner he told me what to do and I did it and 24 hours later he sent me the lottery numbers and I played it I couldn't believe it I won $1,000,000 dollars it's was the best thing that have ever happened to me in my life. If you want to win a lottery WhatsApp or Call Dr Great on this number +2348118829899 or email him at infinitylovespell@gmail.com or infinitylovespell@yahoo.com
CONTACT THE BEST LOTTERY SPELL CASTER FOR THE RIGHT LOTTERY NUMBERS NOW HIS LOTTERY SPELL IS 100% GUARANTEE WHATSAPP +2348118829899
Hello everyone am Raymond from Pennsylvania USA I want to share my wonderful testimony of how a powerful spell caster called Dr Great helped me to win lottery, i have been playing lottery for a long time now but I had no luck everything changed when I messaged Dr Great about winning the lottery he assured me that I will be the next winner he told me what to do and I did it and 24 hours later he sent me the lottery numbers and I played it I couldn't believe it I won $1,000,000 dollars it's was the best thing that have ever happened to me in my life. If you want to win a lottery WhatsApp or Call Dr Great on this number +2348118829899 or email him at infinitylovespell@gmail.com or infinitylovespell@yahoo.com
CONTACT THE BEST LOTTERY SPELL CASTER FOR THE RIGHT LOTTERY NUMBERS NOW HIS LOTTERY SPELL IS 100% GUARANTEE WHATSAPP +2348118829899
Hello everyone am Raymond from Pennsylvania USA I want to share my wonderful testimony of how a powerful spell caster called Dr Great helped me to win lottery, i have been playing lottery for a long time now but I had no luck everything changed when I messaged Dr Great about winning the lottery he assured me that I will be the next winner he told me what to do and I did it and 24 hours later he sent me the lottery numbers and I played it I couldn't believe it I won $1,000,000 dollars it's was the best thing that have ever happened to me in my life. If you want to win a lottery WhatsApp or Call Dr Great on this number +2348118829899 or email him at infinitylovespell@gmail.com or infinitylovespell@yahoo.com
CONTACT THE BEST LOTTERY SPELL CASTER FOR THE RIGHT LOTTERY NUMBERS NOW HIS LOTTERY SPELL IS 100% GUARANTEE WHATSAPP +2348118829899
Hello everyone am Raymond from Pennsylvania USA I want to share my wonderful testimony of how a powerful spell caster called Dr Great helped me to win lottery, i have been playing lottery for a long time now but I had no luck everything changed when I messaged Dr Great about winning the lottery he assured me that I will be the next winner he told me what to do and I did it and 24 hours later he sent me the lottery numbers and I played it I couldn't believe it I won $1,000,000 dollars it's was the best thing that have ever happened to me in my life. If you want to win a lottery WhatsApp or Call Dr Great on this number +2348118829899 or email him at infinitylovespell@gmail.com or infinitylovespell@yahoo.com
DR EMU WHO HELP PEOPLE IN ANY TYPE OF LOTTERY NUMBERS
DeleteIt is a very hard situation when playing the lottery and never won, or keep winning low fund not up to 100 bucks, i have been a victim of such a tough life, the biggest fund i have ever won was 100 bucks, and i have been playing lottery for almost 12 years now, things suddenly change the moment i came across a secret online, a testimony of a spell caster called dr emu, who help people in any type of lottery numbers, i was not easily convinced, but i decided to give try, now i am a proud lottery winner with the help of dr emu, i won $1,000.0000.00 and i am making this known to every one out there who have been trying all day to win the lottery, believe me this is the only way to win the lottery.
Dr Emu can also help you fix this issues
(1)Ex back.
(2)Herbal cure & Spiritual healing.
(3)You want to be promoted in your office.
(4)Pregnancy spell.
(5)Win a court case.
Contact him on email Emutemple@gmail.com
What’s app +2347012841542
Website Https://emutemple.wordpress.com/
Facebook page Https://web.facebook.com/Emu-Temple-104891335203341
You can't win the lottery game without the help of voodoo and this is a fact most people has failed to accept, unfortunately i was one of them until i gave a try trust me if not for security reasons i would have made it public but nevertheless it is not too late to get in contact with Priest Aziba who gave me the spacial lucky numbers i used in playing just once and i won hug amount of money, i would advise you give a try, its not harmful neither is it a sin, its what Africans believe inn and it has also work for me here in the state. VOODOO SPELL LOTTERY NUMBER. Get in contact with Priest Aziba Via Email Priestazibasolutioncenter@gmail.com or WhatsApp him on +2348100368288 so you too can become a millionaire.
Deletethanks this is good blog.
ReplyDeleteInternet Gambling
ReplyDeleteAll the contents you mentioned in post is too good and can be very useful. I will keep it in mind, thanks for sharing the information keep updating, looking forward for more posts.Thanks
adu qq
Excellent Blog! I have been impressed by your thoughts and the way you
ReplyDeletehttps://casinoonlinevenezuela.co.ve
I was pinning away for such type of blogs, thanks for posting this for us. https://juegosdecasinoonlinecolombia.com.co
ReplyDeletePositive site, where did u come up with the information on this posting? I'm pleased I discovered it though, ill be checking back soon to find out what additional posts you include. Latest Thai Lottery King Tips
ReplyDeleteAfter I initially commented I seem to have clicked on the -Notify me when new comments are added- checkbox and now every time a comment is added I receive 4 emails with the exact same comment. There has to be an easy method you are able to remove me from that service? Kudos!
ReplyDeleteTeer Previous rsult 2018
Thank you sooo much for this article. I had the dreadful white screen and your tips saved me .
ReplyDeleteResult
Thai Lottery
I believe a lot of people playing lottery still find it difficult to win, here is a secret i have discovered and it really worked for me i contacted a Spell caster to give me magic numbers and he gave me some instruction which i followed, then he sent the numbers to me which i played and won, today i am a lucky winner of $300,000.00 USD. so i will advise you to get in contact with him and also get a winning number to win hug amount of money Email Priest Aziba via>> Priestazibasolutioncenter@gmail.com and also via his WhatsApp > +(234)81-003-68288
ReplyDeleteI believe a lot of people playing lottery still find it difficult to win, here is a secret i have discovered and it really worked for me i contacted a Spell caster to give me magic numbers and he gave me some instruction which i followed, then he sent the numbers to me which i played and won, today i am a lucky winner of $300,000.00 USD. so i will advise you to get in contact with him and also get a winning number to win hug amount of money Email Priest Aziba via>> Priestazibasolutioncenter@gmail.com and also via his WhatsApp > +(234)81-003-68288
It is really a helpful blog to find some different source to add my knowledge. I came into aware of new professional blog and I am impressed with suggestions of author.
ReplyDeleteหวยฮานอย
WOOOOOOOOOW!I am so happy to shear the goodness of Priest Aziba ,my name is Eric Rodgrigaz a local estate agent now living on the house of my own choice.When I first brought Spell from Email: PRIESTAZIBASOLUTIONCENTER@GMAIL.COM , to win my lotto that was 2018, He showed me how to arrange my winning numbers to win big amount of money . A week later, I my Gfriend went back and matched the spell Lotto numbers to the EuroMillions draw all five numbers matched and i won £81,674.50,I was crazy because I did not put the numbers on the ticket to play but just to try the numbers Priest Aziba gave to me. So, it shows you that this system works. I play all the time now and i always win with the spell of Priest Aziba magic winning numbers. Email at PRIESTAZIBASOLUTIONCENTER@GMAIL.COM And also Write ti his active WhatsApp on +2348100368288 he is really magical telling and giving you all the numbers to play with. I dont have much to say but try his help and be happy like me ERIC forever.
ReplyDeleteI am grateful to you on the grounds that your article is exceptionally useful for me to continue with my exploration in same region. Your cited illustrations are all that much significant to my exploration field.This is extraordinary! It really exhibits to me where to broaden my online diary
ReplyDeleteหวยฮานอย
ReplyDeleteNow that what i am looking for this is very impressive and most advance information that i have seen among different
Shillong Teer Results Blogs and I really liked it.
ReplyDeleteNow that what i am looking for this is very impressive and most advance information that i have seen among different
Shillong Teer Results Blogs and I really liked it.
ReplyDeleteNow that what i am looking for this is very impressive and most advance information that i have seen among different
Shillong Teer Results Online Blogs and I really liked it.
you may find some of the information related to this but this is the most advance information that i have seen among different
ReplyDeleteShillong teer hit lottery Blogs and I really liked it. Love it.
you may find some of the information related to this but this is the most advance information that i have seen among different
ReplyDeleteShillong teer hit lottery Blogs and I really liked it. Love it.
I love the way through which you have secured the information that i have seen among different
ReplyDeleteShillong teer hit Number Blogs and I really liked it. Love it. You nailed it friend
I love the way through which you have secured the information that i have seen among different
ReplyDeleteShillong teer hit Number Blogs and I really liked it. Love it. You nailed it friend
I heard that this blog is very good for the information that is absolutely true thanks alot for sharing it.
ReplyDeleteWin Shillong hit lottery Number
https://drip-designsfurniture.blogspot.com/2016/01/miss-mustard.html?showComment=1554983304117#c2581418148342777862
ReplyDeleteI bet you have some secret source of the information that you have shared with us for the
ReplyDeleteWin Shillong hit lottery Number thanks for sharing this info
ReplyDeleteI like the way through which you have you have shared this information with us and i really liked to share it.
Shillong Teer Number thanks for sharing this info
Have you heard the news that shillong is getting more and more profitable but more tricky and formulated..Thanks for sharing this info
ReplyDeleteShillong Teer Number Loved it and Share it on my wall and my facebook page
This blog aware me about different programs which can become very useful for our friends and kids. Few websites provide combined courses and few of the are separately for single subject. Glad to get this information.
ReplyDeleteหวยฮานอย
Great post I would like to thank you for the efforts you have made in writing this interesting and knowledgeable article. agen judi
ReplyDeleteAn author must have a vast knowledge of vocabulary. The dictionary of a writer must be full of new english vocabulary to make their work more attractive. Use of new words makes their work more valuable and graceful.
ReplyDeleteหวยไทยรัฐ
The golf movie The Legend of Bagger Vance was his next big film, with Smith playing the caddie to Matt Damon's out-of-sorts swinger.poker tournaments
ReplyDeleteI came across many testimonies on net testifying of Dr Aziba a voodoo spell caster that will help you cast a LOTTERY spell and give you the rightful numbers to win the lottery, i didn't believe it, at first but as life got badder i decided to take a try, now my try has made me a millionaire, i have been playing all types of lottery since 7 years now but i have not win up to £1000,after contacting him he cast the spell and give me the hot figures behold i won(£ FOURTY MILLIONS POUNDS) now i am a living testimony of the good works of Dr Aziba A gifted man with a great powers, it is my secret but i decided to make the world known to it as it might be a help to any one who is interested, this happens last week ago you are free to contact him via Gmail> [ priestazibasolutioncenter@gmail com ] And Via WhatsApp [ +2348100368288 ]Am from United kingdom....yours faithful .
ReplyDeletehello i just want to bring to your notice an easy way of becoming a millionaire.I read about a blank ATM card & decided to reach out to this vendor, he then gave me the guidelines & proof of how the card was cloned. Though i wasn’t sure about their services but they assured me of safe & geniue transaction if i obliged to their terms and conditions which i eventually agreed to & 4days later i was delivered a card by the Delivery service which was sent from this hacker. I was shocked when the card dispensed $2000 instant, I've been able to cash out $10k...All thanks to you guys, you can email this real and reliable hacker via email: (verifiedhackinghome.hackers@gmail.com) or whatapp +1 (516) 494 0313 Do view his website to see testimonies of how people became a millionaire by using his BLANK ATM CARD: https://verifiedhackinghomehackers.wordpress.com/
ReplyDeletei am very grateful sharing this great testimonies with you, The best thing that has ever happened in my life is how i win the lottery. I am a woman who believe that one day i will win the lottery.finally my dreams came through when i email Dr Alli . and tell him i need the lottery numbers. i have come a long way spending money on ticket just to make sure i win. But i never know that winning was so easy until the day i meant the spell caster online which so many people has talked about that he is very great in casting lottery spell, so i decide to give it a try.I contacted this man and he did a spell and he gave me the winning lottery numbers. But believe me when the draws were out i was among winners. i win 1.900.000 million Dollar. Dr. Alli truly you are the best, with these man you can will millions of money through lottery. i am so very happy to meet these man, i will forever be grateful to you. Email him for your own winning lottery numbers [ Allispellhelp1@gmail.com ]. OR Whatsapp or Call Via +2348100772528.
ReplyDeleteStraight away after Dr.Alli cast the Lottery spell for me, I felt enveloped by the control of the lotto spell. This spell changes my life into riches. I am now out of debts and experiencing the most amazing good luck with lotto after I won a huge amount of money. I have more luck now than I ever had in my life. i won 1.900.000 million pounds. Your Lotto spell made wonders, I can't believe it. Thank you so much, sir for dedicating your time to cast the Lotto spell for me.”I am eternally grateful for the lotto spell Dr.Alli did for me. You can email him for you own lottery number.email him on
ReplyDeleteAllispellhelp1@gmail.com
WhatsApp +2348100772528
i am very grateful sharing this great testimonies with you, The best thing that has ever happened in my life is how i win the lottery. I am a woman who believe that one day i will win the lottery.finally my dreams came through when i email Dr Alli . and tell him i need the lottery numbers. i have come a long way spending money on ticket just to make sure i win. But i never know that winning was so easy until the day i meant the spell caster online which so many people has talked about that he is very great in casting lottery spell, so i decide to give it a try.I contacted this man and he did a spell and he gave me the winning lottery numbers. But believe me when the draws were out i was among winners. i win 1.900.000 million Dollar. Dr. Alli truly you are the best, with these man you can will millions of money through lottery. i am so very happy to meet these man, i will forever be grateful to you. Email him for your own winning lottery numbers [ Allispellhelp1@gmail.com ]. OR Whatsapp or Call Via +2348100772528.
ReplyDeleteContact Dr Sambo now for Lottery Spell winning numbers Email: divinespellhome@gmail.com
ReplyDeleteDr. Sambo Whats,App. him now +1(267)527-9481 You can also visit his website http://DrSambo443.website2.me My name is Adrienne Bernardo I Live in:New Jersey, I am 55 years old,I want you to know how Dr Sambo helped me, he is do generous with lottery winning numbers, early this year 2019 I contacted him for a Canadian lottery number, he gave me and I won $750,000,000 SEVEN HUNDRED AND FIFTY MILLION DOLLARS I still can’t believe people could have this kind of powers in this modern days. Dr Sambo is the best, he put a smile on my face and my family is rich now. Everybody must be rich, contact Dr Sambo for lucky winning numbers and be rich all your life. Contact him now, it doesn’t matter where you are ,it doesn’t matter your status in life,just contact him and he will sully help you okay...
Thank you for some other informative blog. Where else could I get that type of information written in such an ideal means? I have a mission that I’m just now working on, and I have been at the look out for such information. Read Again
ReplyDeleteHi Guys….I just want to say a big thanks to ( Dr Ogbe ) for what he has done for me and my family by helping me to win lottery. I won Five Hundred and Thirty Three Million Us Dollars. (($533,000,000.00)). His lottery spell is the best and so amazing. My life is now balance and i am Now Very Rich As i have always wanted and i am out of doubt. Are you looking for a real and genuine spell caster to help you win big in any kind of lottery you play? you can contact DrOgbe , today all your plan to ever win Big in Lottery will Come True and work out well for you. His spell very real and genuine i can not still believe it And His spell also work very fast. Thank you so much Dr Ogbe for dedicating your time to cast the Lottery spell for me. I got my bills paid and my debt cleared and am still mega rich. If you need a real And Genuine spell caster to help you Win lottery,kindly contact him for fast and urgent Help Email: drogbeherbalcure5@gmail.com whatsapp numbers +2347063915230THANK YOU FOR READING
ReplyDeleteI came across many testimonies on net testifying of Dr akhigbe a voodoo spell caster that will help you cast a LOTTERY spell and give you the rightful numbers to win the lottery, i didn't believe it, at first but as life got badder i decided to take a try, now my try has made me a millionaire, i have been playing all types of lottery since 7 years now but i have not win up to $1000,after contacting him he cast the spell and give me the hot figures behold i won( FIFTY MILLIONS DOLLARS) now i am a living testimony of the good works of Dr akhigbe A gifted man with a great powers, it is my secret but i decided to make the world known to it as it might be a help to any one who is interested, this happens last week ago you are free to contact him or email him Drakhigbespellhome7@.com) or call 2349021374574
ReplyDeleteI came across many testimonies on net testifying of Dr Sambo spell Home that will help you cast a LOTTERY SPELL and give you the rightful numbers to win the lottery, i didn't believe it, at first but as life got badder i decided to take a try, now my try has made me a millionaire, i have been playing all types of lottery since 7 years now but i have not win up to $1000,after contacting him he cast the spell and give me the hot figures behold i won( THIRTY MILLIONS DOLLARS) now i am a living testimony of the good works of Dr Sambo A gifted man with a great powers, it is my secret but i decided to make the world known to it as it might be a help to any one who is interested, this happens last week ago you are free to contact him or Email him divinespellhome@gmail.com Dr. Sambo WhatsApp him now +2348145810121
ReplyDeleteI came across many testimonies on net testifying of Dr Sambo spell Home that will help you cast a LOTTERY SPELL and give you the rightful numbers to win the lottery, i didn't believe it, at first but as life got badder i decided to take a try, now my try has made me a millionaire, i have been playing all types of lottery since 7 years now but i have not win up to $1000,after contacting him he cast the spell and give me the hot figures behold i won( THIRTY MILLIONS DOLLARS) now i am a living testimony of the good works of Dr Sambo A gifted man with a great powers, it is my secret but i decided to make the world known to it as it might be a help to any one who is interested, this happens last week ago you are free to contact him or Email him divinespellhome@gmail.com Dr. Sambo WhatsApp him now +2348145810121
ReplyDeleteI came across many testimonies on net testifying of Dr Sambo spell Home that will help you cast a LOTTERY SPELL and give you the rightful numbers to win the lottery, i didn't believe it, at first but as life got badder i decided to take a try, now my try has made me a millionaire, i have been playing all types of lottery since 7 years now but i have not win up to $1000,after contacting him he cast the spell and give me the hot figures behold i won( THIRTY MILLIONS DOLLARS) now i am a living testimony of the good works of Dr Sambo A gifted man with a great powers, it is my secret but i decided to make the world known to it as it might be a help to any one who is interested, this happens last week ago you are free to contact him or Email him divinespellhome@gmail.com Dr. Sambo WhatsApp him now +2348145810121
ReplyDeleteHello all my viewers My NAME maria from USA! I am very happy for sharing this great testimonies,The best thing that has ever happened in my life is how I win the euro million lottery. I am a man who believe that one day I will win the lottery.finally my dreams came through when I email Dr clement.and tell him I need the lottery numbers.I have spend so much money on ticket just to make sure I win. But I never know that winning was so easy until the day I mean the spell caster online which so many people has talked about that he is very great in casting lottery spell,so I decide to give it a try.I contacted this great Dr and he did a spell and he gave me the winning lottery numbers. But believe me when the draws were out I was among winners. I win 20,000 million Dollar.Dr. clement truly you are the best,with these great Dr you can win millions of money through lottery.I am so very happy to meet these great man now, I will be forever be grateful to you dr. Email him for your own winning lottery numbers allmightbazulartemple@gmail.com or you can call him for your own help to win big money today whatsap+2347052758952.from maria Banks post (USA)thanks for reading.
ReplyDeleteDr. clement also explain to me he can cure all kind of infection disease with herbal medicine
{1}HIV/AIDS
{2}DIABETES
{3}EPILEPSY
{4} BLOOD CANCER
{5} HPV
{6} ALS
{7} HEPATITIS
{8}LOVE SPELL
{9}if you have problem HighCourt
wow this saintly however ,I love your enter plus nice pics might be part personss negative love being defrent mind total poeple , us greencard lotterie
ReplyDeleteDr. Sambo cast a spell for me per my request. I bought a lottery ticket the day you cast my spell. Guess What guys? I hit 4 of 6 and won 7,000.000.00 Dollars! Then I received a letter from the hospital stating that the $ 7,000.00 bill I owed was settled .I want you to know that, your lottery spell have make me to win millions of dollars. Then a week later I won 100.000.00 thousand dollars,Thank you Dr Sambo for your genuine spell. Am very grateful for what your wonderful lottery numbers did for me, i own a house and a car right now. Am free from debts.thank you for casting the lottery spell for me. I was trying to settle a job action and after the lottery winning spell you did, I received a settlement. I am now self employed. If you are at there looking for a real and a genuine spell caster,search NO MORE. Dr.Sambo is there to help you to win and be rich forever.contact him via his Email: divinespellhome@gmail.com Whats , App. him now +1(267)527-9481
ReplyDeleteCONTACT THE BEST LOTTERY SPELL CASTER FOR THE RIGHT LOTTERY NUMBERS NOW HIS LOTTERY SPELL IS 100% GUARANTEE WHATSAPP +2348118829899
ReplyDeleteHello everyone am Raymond from Pennsylvania USA I want to share my wonderful testimony of how a powerful spell caster called Dr Great helped me to win lottery, i have been playing lottery for a long time now but I had no luck everything changed when I messaged Dr Great about winning the lottery he assured me that I will be the next winner he told me what to do and I did it and 24 hours later he sent me the lottery numbers and I played it I couldn't believe it I won $1,000,000 dollars it's was the best thing that have ever happened to me in my life. If you want to win a lottery WhatsApp or Call Dr Great on this number +2348118829899 or email him at infinitylovespell@gmail.com or infinitylovespell@yahoo.com
CONTACT THE BEST LOTTERY SPELL CASTER FOR THE RIGHT LOTTERY NUMBERS NOW HIS LOTTERY SPELL IS 100% GUARANTEE WHATSAPP +2348118829899
ReplyDeleteHello everyone am Raymond from Pennsylvania USA I want to share my wonderful testimony of how a powerful spell caster called Dr Great helped me to win lottery, i have been playing lottery for a long time now but I had no luck everything changed when I messaged Dr Great about winning the lottery he assured me that I will be the next winner he told me what to do and I did it and 24 hours later he sent me the lottery numbers and I played it I couldn't believe it I won $1,000,000 dollars it's was the best thing that have ever happened to me in my life. If you want to win a lottery WhatsApp or Call Dr Great on this number +2348118829899 or email him at infinitylovespell@gmail.com or infinitylovespell@yahoo.com
ReplyDeleteLottery spells that works immediately.
Is a great thing to announce to the general public for I have been saved and redeemed by winning a power ball lottery with a spell and a winning number from Nanakwakuspiritualist@gmail.com I heard he has helped lot of people until he helped me this month to win my first $500,000 from power ball. You too can try for your self today is just a spell and a winning number. His Whats App number +234 902 990 5501. This just a beginning I will win more,
Good luck. visit website https://lotteryspellsthatworkfast.blogspot.com/
CONTACT THE BEST LOTTERY SPELL CASTER FOR THE RIGHT LOTTERY NUMBERS NOW HIS LOTTERY SPELL IS 100% GUARANTEE WHATSAPP +2348118829899
ReplyDeleteHello everyone am Raymond from Pennsylvania USA I want to share my wonderful testimony of how a powerful spell caster called Dr Great helped me to win lottery, i have been playing lottery for a long time now but I had no luck everything changed when I messaged Dr Great about winning the lottery he assured me that I will be the next winner he told me what to do and I did it and 24 hours later he sent me the lottery numbers and I played it I couldn't believe it I won $1,000,000 dollars it's was the best thing that have ever happened to me in my life. If you want to win a lottery WhatsApp or Call Dr Great on this number +2348118829899 or email him at infinitylovespell@gmail.com or infinitylovespell@yahoo.com
CONTACT THE BEST LOTTERY SPELL CASTER FOR THE RIGHT LOTTERY NUMBERS NOW HIS LOTTERY SPELL IS 100% GUARANTEE WHATSAPP +2347067607558
ReplyDeleteHello everyone am David Carlos from Pennsylvania USA I want to share my wonderful testimony of how a powerful spell caster called Dr EHIJIE helped me to win lottery, i have been playing lottery for a long time now but I had no luck everything changed when I messaged Dr EHIJIE about winning the lottery he assured me that I will be the next winner he told me what to do and I did it and 24 hours later he sent me the lottery numbers and I played it I couldn't believe it I won $1,000,000 dollars it's was the best thing that have ever happened to me in my life. If you want to win a lottery WhatsApp or Call Dr EHIJIE on this number +2347067607558 or email him at (drehijieherbalcenter@gmail.com )
CONTACT THE BEST LOTTERY SPELL CASTER FOR THE RIGHT LOTTERY NUMBERS NOW HIS LOTTERY SPELL IS 100% GUARANTEE WHATSAPP +2347067607558
ReplyDeleteHello everyone am David Carlos from Pennsylvania USA I want to share my wonderful testimony of how a powerful spell caster called Dr EHIJIE helped me to win lottery, i have been playing lottery for a long time now but I had no luck everything changed when I messaged Dr EHIJIE about winning the lottery he assured me that I will be the next winner he told me what to do and I did it and 24 hours later he sent me the lottery numbers and I played it I couldn't believe it I won $1,000,000 dollars it's was the best thing that have ever happened to me in my life. If you want to win a lottery WhatsApp or Call Dr EHIJIE on this number +2347067607558 or email him at (drehijieherbalcenter@gmail.com )
CONTACT THE BEST LOTTERY SPELL CASTER FOR THE RIGHT LOTTERY NUMBERS NOW HIS LOTTERY SPELL IS 100% GUARANTEE WHATSAPP +2347067607558
ReplyDeleteHello everyone am David Carlos from Pennsylvania USA I want to share my wonderful testimony of how a powerful spell caster called Dr EHIJIE helped me to win lottery, i have been playing lottery for a long time now but I had no luck everything changed when I messaged Dr EHIJIE about winning the lottery he assured me that I will be the next winner he told me what to do and I did it and 24 hours later he sent me the lottery numbers and I played it I couldn't believe it I won $1,000,000 dollars it's was the best thing that have ever happened to me in my life. If you want to win a lottery WhatsApp or Call Dr EHIJIE on this number +2347067607558 or email him at (drehijieherbalcenter@gmail.com )
My husband is a very rich and welding man. we make the money together few month later, he started hooking up with bad friends. on my noted he was having an affair with another woman the family lawyer call me an asked me if me and my husband had a miss-understanding because my husband has change the name writing on the wile. he took everything we have to his girlfriend, meaning that i don’t have any share in the family. i was frustrated and discourage. until a friend of my advice me to visit a spell caster so that all my problems will been solve within 48 hours then i contacted the spell caster she introduce to me. Dr Akhigbe (akhigbespellhome@gmail.com) spell-caster, Dr Akhigbe promise that everything will been alright. few weeks later my husband came back home, on his knees begging, asking me to forgive and forget about the past and face the future ahead. right now i am in full control of my husband access. call or Whatsapp dr via +2349035428122 if you are in-need of his help.
ReplyDeleteI came across many testimonies on net testifying of Dr Akhigbe a voodoo spell caster that will help you cast a LOTTERY spell and give you the rightful numbers to win the lottery, i didn’t believe it, at first but as life got harder i decided to take a try, now my try has made me a millionaire, i have been playing all types of lottery since 7 years now but i have not win up to $1000, after contacting him he cast the spell and give me the hot figures behold i won( FIFTY MILLIONS DOLLARS) $50,000 now i am a living testimony of the good works of Dr Akhigbe A gifted man with a great powers, it is my secret but i decided to make the world known too. It might be a help to any one who is interested, this happens last week ago you are free to contact him email: akhigbespellhome@gmail.comWhatsApp number +2349035428122
ReplyDeleteI am very happy for sharing this great testimonies,The best thing that has ever happened in my life is how I won the lottery euro million mega jackpot. I am a man who believe that one day I will win the lottery. finally my dreams came through when I email Dr KABAKA. and tell him I need the lottery numbers. I spend so much money on ticket just to make sure I win. But I never knew that winning was so easy until the day I meant the spell caster online which so many people has talked about that he is very great in casting lottery spell, . so I decide to give him a try. I contacted this great Dr KABAKA and he did a spell and gave me the winning lottery numbers. But believe me when the draws came out I was among the lucky winners. I won(£100,000 one hundred thousand Pounds) Dr KABAKA truly you are the best, with these great Dr you can win millions of money through lottery. I am so very happy to meet these great man, I will be forever grateful to you dr. KABAKA, if you are out there looking for his help you can reach him for easy communication on Whatsapp +2349015857861 or email him via his email drkabakaspiritualtemple@gmail.com
ReplyDeleteI am very happy to share this great testimonies,The best thing that has ever happened in my life is how I won the lottery euro million mega jackpot. I am a man who believes that one day I will win the lottery. Finally my dreams came through when I email Dr Akhigbe. and tell him I need the lottery numbers. I spend so much money on tickets just to make sure I win. But I never knew that winning was so easy until the day I meant the spell caster online which so many people have talked about that he is very great in casting lottery spells, so I decided to give him a try. I contacted this great Dr Akhigbe and he did a spell and gave me the winning lottery numbers. But believe me when the draws came out I was among the lucky winners. I won(£100,000 one hundred thousand Pounds) Dr Akhigbe truly you are the best, with these great Dr you can win millions of money through lottery. I am so very happy to meet these great men, I will be forever grateful to you dr. Aba, if you are out there looking for his help you can reach him for easy communication on Whatsapp +2349035428122 or email him via his email Akhigbespellhome@gmail.com
ReplyDeleteMoney Spell Win Lottery spell Business spell | Lotto spell call +2348158836673
ReplyDeleteWhen you do not have the financial freedom to do as you wish life can take a toll on you and your family.
Money spell can help increase financed in many ways. We can help with business spells, lottery spells, getting people to pay you back and gambling spells.
Little Lottery Spell- Are you looking for a jackpot win on either a scratch off ticket or the little lottery? This spell can be directed at either type of lottery game in your area to produce a onetime jackpot win. Better Odds Gambling Spell - Do you go to the casinos and gamble frequently?
This spell will increase the odds of your natural win when you go to gamble. You will see larger, more frequent wins.
Double Power Gambling Spell - Are you a big gambler and want to make sure that you win over and over?
This spell will bring several large wins at the casino playing table games and slot machines. Dr olokum call/whatsapp his Africa branch on +2348158836673 email him on drolokumspelltemple@gmail.com
HOW I WON £4,369,877 WITH DR TRUST LOTTERY MAGIC SPELL
ReplyDeleteI am James Couper From the UK...I had to write back and say what an amazing experience I had with Dr Iheme powerful lottery spell. My Heart is filled with joy and happiness after Dr Trust cast the Lottery spell for me, And i won £4,369,877. His spell changed my life into riches, I'm now out of debts and experiencing the most amazing good luck with the lottery after I won a huge amount of money. My life has really changed for good. I won (Four million three hundred and sixty nine thousand Eight hundred and seventy seven thousand pounds)Your Lottery spell is so real and pure. Thank you very much Dr. Trust for the lottery spell that changed my life”I am totally grateful for the lottery spell Dr Trust did for me. You can email him for your own lottery number,because this is the only secret to Win the lottery.
Email him: ihemesupernaturaltemple@gmail.com
WhatsApp or Call him +2348167061171
HOW I WON £4,369,877 WITH DR TRUST LOTTERY MAGIC SPELL
ReplyDeleteI am Hiltom From the UK...I had to write back and say what an amazing experience I had with Dr Iheme powerful lottery spell. My Heart is filled with joy and happiness after Dr Trust cast the Lottery spell for me, And i won £4,369,877. His spell changed my life into riches, I'm now out of debts and experiencing the most amazing good luck with the lottery after I won a huge amount of money. My life has really changed for good. I won (Four million three hundred and sixty nine thousand Eight hundred and seventy seven thousand pounds)Your Lottery spell is so real and pure. Thank you very much Dr. Trust for the lottery spell that changed my life”I am totally grateful for the lottery spell Dr Trust did for me. You can email him for your own lottery number,because this is the only secret to Win the lottery.
Email him: ihemesupernaturaltemple@gmail.com
WhatsApp or Call him +2348167061171
TESTIMONY ON HOW I GOT MY LOAN FROM A GENUINE FINANCE COMPANY LAST WEEK. Email for immediate response: drbenjaminfinance@gmail.com
ReplyDeleteI am Mrs,Leores J Miguel by name, I live in United State Of America, who have been a scam victim to so many fake lenders online between November last year till July this year but i thank my creator so much that he has finally smiled on me by directing me to this new lender who put a smile on my face this year 2020 and he did not scam me and also by not deceiving or lying to me and my friends but however this lending firm is BENJAMIN LOAN INVESTMENTS FINANCE (drbenjaminfinance@gmail.com) gave me 2% loan which amount is $900,000.00 united states dollars after my agreement to their company terms and conditions and one significant thing i love about this loan company is that they are fast and unique. {Dr.Benjamin Scarlet Owen} can also help you with a legit loan offer. He Has also helped some other colleagues of mine. If you need a genuine loan without cost/stress he his the right loan lender to wipe away your financial problems and crisis today. BENJAMIN LOAN INVESTMENTS FINANCE holds all of the information about how to obtain money quickly and painlessly via Call/Text: +1(415)630-7138 Email: drbenjaminfinance@gmail.com
When it comes to financial crisis and loan then BENJAMIN LOAN INVESTMENTS FINANCE is the place to go please just tell him I Mrs. Leores Miguel direct you Good Luck....
My ex-husband and I had always managed to stay friendly after our divorce in February 2017. But I always wanted to get back together with him, All it took was a visit to this spell casters website last December, because my dream was to start a new year with my husband, and live happily with him.. This spell caster requested a specific love spell for me and my husband, and I accepted it. And this powerful spell caster began to work his magic. And 48 hours after this spell caster worked for me, my husband called me back for us to be together again, and he was remorseful for all his wrong deeds. My spell is working because guess what: My “husband” is back and we are making preparations on how to go to court and withdraw our divorce papers ASAP. This is nothing short of a miracle. Thank you Dr Emu for your powerful spells. Words are not enough. here is his Email: emutemple@gmail.com or call/text him on his WhatsApp +2347012841542
ReplyDeleteHe is also able to cast spell like 1: Lottery 2: Conceive 3: Breakup 4: Divorce 5: Cure for all kinds of diseases and viruses.
This blog was extremely helpfull. I really appreciate your kindness in sharing this with me and everyone else! số đá miền nam là gì 188loto
ReplyDeleteAwesome article, I am a big fan of this website, keep on posting that great content, and I'll be a regular visitor for a long time...looking for the next one....keep it up! mơ thấy tai nạn đánh con gì ăn lớn
ReplyDelete
ReplyDeleteDear Sir/Ma
I am a veteran with common wealth of nations humanitarian delivery agency a subsidiary of UN..
My colleague died of covid19. Before her death she left in the sum of (€17,000,000.00) with a Security & Finance Firm in Europe for safe keeping there is an incrustation she reviled that the funds should not be left unclaimed. You are to stand as the beneficiary to late Sarah Hayes.
Respond to me your interest at lampealfredm46@gmail.com,and contact details for all other formalities which is genuine and trustworthy person.
Hoping to have a good deal with you on mutual trust.
Sincerely,
ReplyDeleteDear Sir/Ma
I am a veteran with common wealth of nations humanitarian delivery agency a subsidiary of UN..
My colleague died of covid19. Before her death she left in the sum of (€17,000,000.00) with a Security & Finance Firm in Europe for safe keeping there is an incrustation she reviled that the funds should not be left unclaimed. You are to stand as the beneficiary to late Sarah Hayes.
Respond to me your interest at lampealfredm46@gmail.com,and contact details for all other formalities which is genuine and trustworthy person.
Hoping to have a good deal with you on mutual trust.
Sincerely,
I WON LOTTERY WITH THE HELP OF DR ISIKOLO. YOU TOO CAN WIN LOTTERY OR LOTTO JACKPOT.
ReplyDeletei am very grateful sharing this great testimonies with you, The best thing that has ever happened in my life is how i win the lottery. I am a woman who believe that one day i will win the lottery. finally my dreams came through when i email Dr ISIKOLO . and tell him i need the lottery numbers. i have come a long way spending money on ticket just to make sure i win. But i never know that winning was so easy until the day i meant the spell caster online which so many people has talked about that he is very great in casting lottery spell, so i decide to give it a try. I contacted this man and he did a spell and he gave me the winning lottery numbers. But believe me when the draws were out i was among winners and i won $745,000USD. DR ISIKOLO truly you are the best, with these man you can will millions of money through lottery. i am so very happy to meet this man, i will forever be grateful to you.
You need your lover back to you.
you need cure for sickness and diseases.
you need good luck charm or protection spell.
winning of any games to become rich.
He can help you so contact him with his Email: isikolosolutionhome@gmail.com or WhatsApp him on +1(725)240-4536
My name is Robert Evans, I am very grateful sharing this great testimonies with you, The best thing that has ever happened in my life is how i won the lottery. I am a man who believe that one day i will win the lottery finally my dreams came through when i email Dr.Noruwa and told him i need the lottery numbers. i have come a long way spending money on ticket just to make sure i win. But i never knew that winning was so easy until the day i meant the spell caster online which so many people has talked about that he is very great in casting lottery spell, so i decided to give him a try. I contacted this man and he did a spell and he gave me the winning lottery numbers. But believe me when the draws were out i was among winners. i won 70,912,673.20 million Dollar. Dr.Noruwa truly you are the best, with these man you can win millions of money through lottery. i am so very happy to meet these man, i will forever be grateful to you. Email him for your own winning lottery numbers his Email: doctornoruwavickyhealingtemple@gmail.com Or chat him on Telegram/ WhatsApp: +1(562)774-3626
ReplyDeleteNice Post Your content is very inspiring and appriciating I really like it please visit my site for Satta King and Satta king Charts or for super fast result satta matka also checkout my site Lottery Sambad you can also visit out site satta king result visit us on satta king faridabad satta king ghaziabad my new site SattaKing
ReplyDeleteप्ले बाजार, सत्ता किंग, दिसावर सत्ता , फरीदाबाद सत्ता, श्री गणेश , ताज , आगरा प्ले बाजार , सत्ता मटका मार्किट इस ओने ऑफ़ थे world'स मोस्ट फेमस सत्ता मटका एंड सत्ता मटका गेम्स. मान्य पीपल अराउंड थे वर्ल्ड हैवे प्लाएड थिस गेम. Satta King
ReplyDeleteBEST LOTTERY SPELL BY POWERFUL DR. OBINNA
ReplyDeleteI use to be a very poor man who has always not find luck when it comes to playing the lottery. I have been playing lottery since i was 21 years and now i am 52 meaning i have been playing lottery for 31 years. The biggest amount i have ever won in my life was 400 bucks. But one day my story turns to history after i find this man name DR. OBINNA on the Internet that he is the best when it comes to winning lottery. This man is a very strong voodoo doc who gives out the numbers that can never fail. After all my years of laboring and struggling to win the lottery i finally won ( $62,000,000) with the help of DR. OBINNA lottery spell. email him now to get the best lottery number to win big amount of lottery All thanks to Dr OBINNA His contact informations...
Email: obinnaspelltemple@yahoo.com
His WhatsApp +19492293867.
I am Larry Baier. I can never stop thanking Dr Graceondu for transforming my life, i have been paying lottery games for a very long time and i have never one day win any game, i met a friend whom i complained to about my inability to win and he introduced me to Dr Graceondu whom helped his life by giving him a game that he played and he won $150,000
ReplyDeleteso i contacted him through his email and he assured me that i will wine big once he give me a game to play, he asked me to give him two day so he can make prayers to his gods so that the winning numbers will be revealed to him, so i waited for the two days the second day he sent me the number to play, so i went to play the game i never had it in my mind that i was going to win such amount of money, so on that faithful day i went to check the game on April 16, 2021 and behold i got the biggest shock of my life i won $2,000,000 and from that moment my life changed.
all thanks to Dr Graceondu, i want to also advice everyone out there to also contact him if you have been playing lottery and you have never won.
You can reach him via his email, drgraceondu12@gmail.com or WhatsApp him @ +15204677763
Great post! Enjoy Sportsbook & live casino games which are exciting, promising & rewarding. Play Online Casino Singapore game today!
ReplyDeleteReally I enjoy your site with effective and useful information.
ReplyDeletelive casino singapore
Hello viewers, i am Rosaline Comma, from USA, i want to use this opportunity to thank Priest Bacasim for the great work he has done in my life. I had a very big misunderstanding with my husband and he said he do no longer want me again that he needs a divorce, i was heart broken, i was diverstated and confused, i didn't know what to do until one faithful day i saw a testimony of someone testifying about what Priest Bacasim has done for her i never believed in magic or spell but i had no choice, i decided to give it a try, so i contacted him via his email (pristbacasim2000@gmail.com) he told me what i need to do which i did and he promised me that within 48 hours my husband was going to contact me, i didn't believed it 100%, so the second day morning as i was preparing to go to work i had my phone ring and i went to pick it up i was surprise it was my husband calling, i answered and he started apologizing to me, i forgave him because i love him so much, and now he has turned a new live he stopped all the bad things he used to do, now he loves me more than he used to before. You can also contact him if you are also passing through and kind of marital problem or relationship issues he is a very powerful spell caster and i believe he will help you too pristbacasim2000@gmail.com or you can also WhatsApp him on +15202103368 or visit his website on https://priestbacasima2001.wixsite.com/priest
ReplyDeleteDo you need an urgent loan of any kind? Loans to liquidate debts or need to loan to improve your business have you been rejected by any other banks and financial institutions? Do you need a loan or a mortgage? This is the place to look, we are here to solve all your financial problems. We borrow money for the public. Need financial help with a bad credit in need of money. To pay for a commercial investment at a reasonable rate of 3%, let me use this method to inform you that we are providing reliable and helpful assistance and we will be ready to lend you. Contact us today by email: daveloganloanfirm@gmail.com Call/Text: +1(501)800-0690 And whatsapp: +1 (501) 214‑1395
ReplyDeleteNEED A LOAN?
Ask Me.
This comment has been removed by the author.
ReplyDeleteThe price of sugarcane should be declared at Rs 450 a quintal. He has demanded from the Chief Minister to declare the price of sugarcane at Rs 450 before running the sugar mill.
ReplyDeleteSatta King
Satta Result
Margaret Loughrey
ReplyDeleteI never thought that I could be this wealthy after all I've been through trying to meet ends and take care of my family, I used to play lottery but has never be lucky to win until I saw some comments online how he had helped a lot of people win, after first I didn't believe him but still I gave it a try, I wrote him a message on email after few hours he replied back so I told him what I want he assured me success. he also told me what I should do and I did all he requested from me, after some hours he gave me the lucky numbers and showed me where to play so i did as instructed to my biggest surprise I won 27 million pounds (Euromillions). Now I'm rich and happy all thanks to Dr Benjamin for the help, I'm nothing without you. if you need his help to win you can reach him via his email drbenjaminlottospell711@gmail.com and his whatsapp +13344539570 or visit his website Drbenjamintemple.com
ACP pashchim va esapee sauth kee teemon ne phajalaganj, kaakaadev va najeeraabaad mein sanyukt roop se chhaapa maarakar aaipeeel maichon par chal rahe satte ke khel ka pardaaphaash kar kareeb 94 laakh rupaye nakad baraamad kie the.
ReplyDeleteSatta King
Satta Result
Satta Result
Hi everyone, after 10 years of playing lotto game i am finally living my dream life, all thanks to Dr Dominion i will never forget that great man never in my entire life, i am who i am today all because of him he gave me a winning numbers to play and he prepared a lotto winning spell for me that helped me won my mega million. thank you so much Dr Dominion for what you have done for my entire generations, i will forever be grateful.
ReplyDeleteyou can reach out to him on his info:
Email: dominionlottospelltemple@gmail.com
WhatsApp: +16574277820
this is real take it serious, who will believe that a herb can cure ten
ReplyDeleteyears HIV in my body, i never believe that this will work i have spend a
lot when getting drugs from the hospital to keep me healthy, what i was
waiting for is death because i was broke, one day i hard about this great
man who is well know of HIV and cancer cure, i decided to email him,
unknowingly to me that this will be the end of the HIV aids in my body, he
prepare the herb for me, and give me instruction on how to take it, at the
end of the two week, he told me to go to the hospital for a check up, and i
went, surprisingly after the test the doctor confirm me negative, i thought
it was a joke, i went to other hospital was also negative, then i took my
friend who was also HIV positive to the Dr voodoo after the treatment she
was also confirm negative . He also have the herb to cure cancer please i
want every one with this virus to be free, that is why am dropping his
email address, voodoospelltemple66@gmail.com i want you to email him he
is a great man. the government is also interested in this Dr voodoo
thank you for saving my life, and I promise I will always testify
for your good work you can also add him on whatsApp
+2348140120719
I loved to read blogs and your blog is one of the best blog.Sattaking
ReplyDeleteI used to be able to find good information from your blog posts.Sattaking
ReplyDeleteGET YOUR EX LOVER BACK NOW OR GET YOUR BROKEN RELATIONSHIP, MARRIAGE RESTORED.
ReplyDeleteI’m just upset that I have been in pain and crying for so long and many times. Thank you dromokpo@gmail.com
I wished I would have found you earlier, you would have saved me from a lot of pain for the past five years my ex lover left me for another woman in just 2 days i contacted you Dr Omokpo you brought my broken relationship back
I spent a small fortune enough to take my dream trip to South Carolina but what’s the point in taking a dream trip without the love of my life. Dr Omokpo has given me hope and his honesty is a breath of fresh air, I feel so good and heavy happiness in my heart to get my ex lover back. Who I thought he was gone forever. We are married now as I share my testimony with you. If you have broken relationship or broken marriage or you want to get your ex lover back kindly contact: dromokpo@gmail.com
ReplyDeleteI used to be able to find bestv and so better good information from your blog post.
satta king result
TO WHOM IT MAY CONCERN DR LOJA IS REAL.
ReplyDeletemy name is Bemjamin from UK (London) my wife has heard rumors about me and this issues made her filed for divorce and everything went up up and this case and the thought of losing my family now has kept my heart unhappy so i prayed for a solution and a way i can be able to bring back my wife and kids back and prove to her all these things she heard about me and the other lady working in my office are all lies because deep down in my heart i knew i never and will never cheat on my wife. to cut this whole story short my wife sister from the USA heard all the issues in ground and immediately asked me to contact DR LOJA she gave me his contacts details and i did as she said and DR LOJA told me everything will be fine in two days in two days my wife will come home for good again and this was exactly what happened and for this reason i say this man is real and can also help anyone with any of the below problem
BRINGING BACK LOST LOVER.
RESTORATION OF BROKEN MARRIAGES / RELATIONSHIPS.
HEALING OF DISEASES.
PRAYERS OVERCOME SPIRITUAL ATTACKS OR BAD DREAMS.
CURE FOR HSV 1 AND HSV 2.
TOTAL FOR INFECTION STD ETC.
A WEEK TREATMENT AND CURE FOR HIV IS GAURANTEED.
PRAYERS FOR LUCKY NUMBERS FOR LOTTERIES WINNING.
ETC......................
https://web.facebook.com/Drlojasolutions1000000/
email;drlojasolutions@gmail.com
call/ text/ whatsapp ; +2349159144552
Good day everybody, This is my testimony on how i won $4,200,201 million I want to use this opportunity to thank Great Priest Salami for helping me to win the lottery of $4,200,201 million dollars on Mega millions lottery ticket. I have been playing the lottery for the past 10 years now and I have never won. Ever since then I have not been able to win and I was so upset and I needed help to win the lottery. So I decided to go online and search for help, there i saw so many good testimonies about this man called Great Priest Salami of how he has cast lucky spell lotto for people to win the lottery. I contacted him also and told him I want to win a lottery, he cast a spell for me which I use and I played and won $4,200,201 million dollars. I am so grateful to this man, just in-case you also need him to help you win, you can contact him through his email: purenaturalhealer@gmail.com WhatsApp number +2348143757229
ReplyDeleteI'm Thomas Yi from the United States. I started playing lottery games 3 years ago and I have never won big. I went online to seek help on how I can win big in my lottery games and I saw some nice reviews about Dr Amber who has made different people huge winners in their lottery games with his prayers. I gave it a try and I contacted Dr Amber who told me how and what to do before I can become a big lotto winner and I accepted. He made special prayers for me at his temple and gave me the required numbers to play the lotto game and when I played it, I won a massive $235.4 million POWERBALL jackpot. I was so happy and I chose to receive my winnings in a one-time, lump-sum payment of $160,038,447.27 at Florida Lottery Headquarters in Tallahassee and the balance was given to the store that I bought & played the game from. I would love other people to seek help from him and he can be contacted through WhatsApp/call/text via this number +1 (406) 646-2222 or you can email him on: amberlottotemple@yahoo.com
ReplyDeleteI'm Melvin Martins. from the United States. I started playing lottery games 7 years ago and I have never won big. I
ReplyDeletewent online to seek help on how I can win big in my lottery games and I saw some nice reviews about Dr John who has
made different people huge winners in their lottery games with his prayers. I gave it a try and I contacted Dr John who
told me how and what to do before I can become a big lotto winner and I accepted. He made special prayers for me at his
temple and gave me the required numbers to play the lotto game and when I played it, I won a massive $235.4 million
POWERBALL jackpot. I was so happy and I chose to receive my winnings in a one-time, lump-sum payment of $160,038,447.27
at Florida Lottery Headquarters in Tallahassee and the balance was given to the store that I bought & played the game
from. I would love other people to seek help from him and he can be contacted through WhatsApp/call/text via this
number +1 (803) 820 2671 or you can email him on: Drjohnwinlotterspell@gmail.com .
There is a great PSYCHIC that gives lottery winning numbers to people. I won $739,342,000 Million dollars with the help of his winning numbers, I have been playing lottery games for years and I have never been lucky but my Friend in the office won 496,800.000 million dollars and resigned from work so I beg him for help and he said lord Bubuza predicted his winning after casting a spell and gave him the winning number to play and he won so I spoke to lord Bubuza on WhatsApp: +1 984 240 7211 for help. He responded and said a reading had to be done and a spell cast to reveal my SIX winning numbers, I provided his requirements for the reading and casting of the spell. After casting the spell, he gave me SIX numbers and said it’s my winning number and told me when and where to play it. I did as instructed and 24 hours later, I got a call that I won $739,342,000 million dollars, I thought it was a joke until the amount hit my bank account. Lord Bubuza can help you win too. Contact him via WhatsApp: +1 984 240 7211 or email: lordbubuzamiraclework@hotmail.com
ReplyDeleteLottery is something majority of the people in the world want to win, not only winning the lottery, but they want to win big, i have been playing the lottery for couple of years now, but i haven,t really win big, personally i always think there is something behind all those winners who always win big, because my intense always tell me that every thing is possible, i manage to get in contact with one of the biggest lottery winner in the US, i asked him about the success, and he referred me to a very powerful voodoo doctor, (Dr Emmanuel), he is indeed a great man who i explained to , without no hidden details , (i really want to win the lottery so bad ) he put to work and few days latter he gave me numbers that never fails , these numbers was what i played and i won $1,000,000,00, 1 Million Dollars , (Dr Emmanuel) is blessed , you too can change your life too with his help, contact Email: dremmanuellottoryspellcaster@gmail.com
ReplyDeleteAre you having issues in your relationship, or finding it difficult to have a child of your own or are you the type having any diseases in your body. I will advice you to contact Dr. Abolo of Abolospell@gmail.com . The potency of his spell is so effective and can reunite broken relationship and can also make one get pregnant know matter the situation and not only that, he also has the power to cure all type of diseases within the period of 48hours.. Contact him today and thank me later.
ReplyDeleteContact details : Abolospell@gmail.com
You can also send him a MSG on whatsapp directly via: +447535135409.
Worry no more about how to win big in your lottery game for Dr Amber is able to give you sure winning numbers to win big on your lottery games for I am a winner of $360,000,000. Email: amberlottotemple@yahoo.com or WhatsApp him on +1 (318) 306-5044 for more information.
ReplyDeleteThere aren’t enough words to describe or explain my wonderful experience with CYBERCREDITGURU a US based Russian h a c k e r s. In 2018, I had 205 BTC in my blockchain wallet but out of my carelessness I misplaced my password and recovery phrase. I really don’t know how to go about it until early this year, I came across a 5star review about them in a forum online by one Mrs. Kimberly and I reached out to them via text: +1 (650) 439 0624 and CYBERCREDITGURU (AT) GMAIL DOT COM. They responded immediately and helped recovered my lost BTC wallet within 4 days. Thanks to Team CyberGuru. I also had an extremely poor credit report of 403 with derogatory; late payment, repossession, collections and foreclosure. They also cleared all negative items from my credit report and upgraded my FICO score to 810 across all three major bureaus. Now with no doubts I can say 2022 is a great year for me as I am a proud owner of a new house and a car. All thanks to CYBERCREDITGURU once again. They are my messiah! I confidently recommend them to you.
ReplyDeleteNice Post
ReplyDeleteGood Information you are provided. Thanks for this post and keep posting.
Ac maintenance in delhi
Ac repairing in delhi
Ac Service in Delhi
AC Installation Service in Delhi
I never thought I would be known for winning the lottery in NEW YORK. I am so grateful to DR AMBER for all he has done for me. I wouldn't have been able to win a CENT on the lottery if not for the help of DR AMBER who gave me perfect winning numbers to play the lottery that made me the winner of $10,000,000 DOLLARS in 2019. I got in touch with him again on his webpage: [ https://amberlottotemple.com ] in request for sure winning numbers to play the lottery. He told me what to do and I did all he instructed & required to get the spell prepared for me and within 3 days, he gave me the perfect numbers to play the lottery and could you believe that I won $10,000,000 DOLLARS after playing the lottery making it the second time I have won and I haven't finished spending the last one I won in 2019. DR AMBER is truly a God sent and I highly recommend him to anyone that needs help to win the lottery. You can message him on WhatsApp with +1 318-306-5044 or email: amberlottotemple@yahoo.com
ReplyDeleteJUAN HERNANDEZ FROM UNIONDALE NEW YORK, USA.
India's No.1 Matka Site (Satta matka) Heartly Welcome. Here You Will Get Perfect Guessing By Cm satta matkaTop Guesser And Fast Matka Result. Aaj Ka Satta Kalyan Fix Single Jodi Free Update Here You Find Top Matka Market Of By App Best Matka Site By Satta matka.
ReplyDeleteranthambore national park is one of the best place o view wild animals sanctuary. Visitors can view wild animals at best view nearest view. Visitors can click pictures on best view.
ReplyDeleteDhankesari Nagaland State Lottery Sambad Result 1:00 PM
ReplyDeletehttps://dhankesariresults.in/dhankesari-lottery-result-11-55-am.html
Good day to you reading this now. I am very happy to share my insight working with DR AMBER because his powerful spell made me financially buoyant that no bill scares me anymore after winning 87 MILLION DOLLARS from the lottery game I played with your sure winning numbers. I want to thank DR AMBER for his endless help and he's from the United States. For urgent response, Call or text +1 808 481 5132 or email: amberlottotemple@yahoo.com or visit: AMBERLOTTOTEMPLE.COM
ReplyDeleteHello folks, I want to share my story of how I met Dr Amber who helped me win the lottery. Before I met him, life was hard for me. I love playing the lottery but I lost all my money to it. I became suicidal because I owe the bank lots of money. So, I went on the internet about how I can win the lottery and I got good advocacy about Dr Amber and his work. I got in touch with him and I told him what I’ve been through and he assured me that he will help me. I was a bit scared but I said ok. Dr Amber made a spell for me that cost me some money to get it done and I was given some accurate digits by him to play the lottery on my next game which I did as instructed by him. I was astonished when I got announced as the winner of $109 million dollars on the Mega Millions Lottery I played. I am grateful to Dr Amber for Indeed, he deserves the hype he gets from people. You can email him or visit his webpage on how to get yours done. Email: amberlottotemple@yahoo.com or visit: amberlottotemple.com
ReplyDeleteDownload latest movies in full HD quality only on moviesjaggat. This website offers latest movies, TV shows and Websries in HD print like Drishyam 2 Movie Download filmyzilla 480p 720p 1080p, Doctor G Movie Download Filmyzilla Leaked 480p 720p 1080p and Avatar 2 Movie Download
ReplyDeleteIndia's Largest B2B Marketplace for Footwear Manufacturers & Suppliers
ReplyDeleteFind reliable wedding dress manufacturer, wedding dress wholesaler & supplier on Shoppa.In.
Brilliant post. Very useful.
ReplyDeleteIf you can take out some time to check this.
Mutual funds allow you to invest in a variety of different securities (e.g., stocks, bonds, etc.) with a single investment. This will help you to spread risk and gain maximum benefit. You can open your Demat Account online.
Ias Score launched ncert foundation classes in delhi for proper guidance and provide quality education to UPSC student. One of the unique features of these Classes is its focus on NCERT-based syllabus for UPSC
ReplyDeleteI never thought I could be this wealthy, after all I've been through trying to raise money and take good care of my family. I used to play the national lottery but have never been lucky! One day I read an article by someone named "Bran's mahan", on the internet how he was guided by a Man and became a lottery winner, I decided to contact the spellcaster to help me win too. He gives me full assurance that he will help me win the lottery, but I've to meet his requirements which I did. After some days he gives me some numbers to play. Which I played! I was in my sitting room when I read the notification and it said I had won £1M but I didn't really believe it. I quickly picked up my phone and called the national lottery and even when I heard the word ' Congratulations you're a winner' - I just couldn't take it in. My wife came down from upstairs when she saw me in tears on the phone. She thought I'd been scammed or something bad had happened though it was tears of joy, that very day was a blessing to me. On my way to tell my family members about my win, I discovered I had won £5 on another national lottery ticket I bought on a whim, all thanks to God and Dr Marcus for making my dreams come through. Reach Dr Marcus on his Whatsapp+2348110492028 on email drmacusspellcaster@gmail.com and I believe he will guide you too.
ReplyDeleteJivan Sahayata has curated an impressive collection of resources to help individuals navigate life's challenges. The insights and tips provided here are both insightful and practical, making this site a must-visit.
ReplyDeleteGS SCORE- The nature of UPSC Civil Services Exam has changed tremendously in the past few years. The CSAT Paper has been of qualifying nature since 2015. However the paper pattern of UPSC CSAT is undergoing constant internal changes and getting tougher within those 80 questions that form this paper making it tougher to score even 33% marks CSAT course for UPSC IAS Prelims. GS SCORE provides CSAT Previous Year Papers With Solutions and Csat Syllabus.GS SCORE UPSC CSAT for your preparation. Join now!!
ReplyDeleteYou can't win the lottery game without the help of voodoo and this is a fact most people has failed to accept, unfortunately i was one of them until i gave a try trust me if not for security reasons i would have made it public but nevertheless it is not too late to get in contact with Priest Aziba who gave me the spacial lucky numbers i used in playing just once and i won hug amount of money, i would advise you give a try, its not harmful neither is it a sin, its what Africans believe inn and it has also work for me here in the state. VOODOO SPELL LOTTERY NUMBER. Get in contact with Priest Aziba Via Email Priestazibasolutioncenter@gmail.com or WhatsApp him on +2348100368288 so you too can become a millionaire.
ReplyDeleteIf you're looking for European Champion English Golden Retrievers in Chicago, you're in for a treat! These puppies are known for their gentle temperament and gorgeous, light-colored coats. Perfect family companions!
ReplyDeleteGood day viewers, I wish to share my testimony with all of you. I have daily 9 to 5 jobs, but while I work, I try my luck at playing instant Lotto. On this particular day, I decided to seek help online regarding tips for winning the lottery, and I saw many individuals testifying about Meduza spells. I reached out to him and informed him that I needed help to win the lottery, and he clarified the process to me, stating that after he casts the spell, it will take 48 hours for him to provide me the winning numbers, which I accepted. I followed all his instructions, and he provided me with the numbers to enter the Lottery. After the draw the following morning, I received a notification on the Lottery app on my phone indicating that I was the lucky winner of $273 million on the New Jersey Lottery and I'm here to extend my heartfelt gratitude to Meduza. If you seek for assistance in any aspect of your life, WhatsApp Meduza via: +1 (807) 907-2687 or Email: lordmeduzatemple@hotmail.com
ReplyDeleteI am so excited to share with you how Dr Marcus made me achieve my dreams after 10 years of playing the lottery. I saw a couple of comments about him several years ago. I wondered how it was possible. Until it finally works for me the numbers he gave me were what I played, I'm still in shock. I, a Lapeer county man, won the $1,000,000 power ball, the only word I can use to describe the feelings of finding out that I have won the 1 million dollars is shocking. I am just now believing that this is real. dr marcus is indeed a powerful man you can reach him at drmacusspellcaster@gmail.com or whatsapp him at +2348110492028 i am working to get more wins 😊
ReplyDeleteI've been attempting to expand my wine business in my hometown in White Plains. For the past 7 years, I do play the lottery in my spare time, but on this blessed day I came across an article about Lord Meduza's spell to win the lottery. I contacted Lord Meduza to see if it would work and after I agreed to his terms and conditions for completing the task for me, he performed his magical powers for me and within 48 hours, he provided me with the numbers I needed to play the lottery, and I followed his directions. I found out at the store that I was the winner of a $105 million jackpot. For a moment I felt uncertain but I looked again and I saw it was real. As I speak to you, My level has been elevated from grass to grace and I've come to know that life is more spiritual and with the Lord Meduza spell, you can actually win the lottery. Please assist me in thanking him and his contacts are listed below
ReplyDeleteWhatsApp: +1 (807) 907-2687
Email: lordmeduzatemple@hotmail.com
GaliResult की मदद से मैंने अपने Sattaking के नंबर guess करना और आसान बना लिया है। बहुत उपयोगी जानकारी मिलती है।
ReplyDeleteMain pehle doosri websites par jaata tha results ke liye, lekin jab se Satta King mila hai, kahin aur dekhne ka mann hi nahi karta. Yahan sab kuch real-time aur clearly updated milta hai.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteइस लेख ने मुझे Sattaking को एक नई नजर से देखने का मौका दिया। मैं GaliResult को रोज़ देखता हूं लेकिन अब इसकी अहमियत और ज्यादा समझ में आई।
ReplyDeleteFAQs सेक्शन ने बहुत सारे संदेह दूर कर दिए। यह आर्टिकल नए खिलाड़ियों के लिए बहुत उपयोगी है।
Sattaking beginners ke लिए advice – पहले daily Sattareport ज़रूर देखो, तभी samajh aayega kaunse number trend में हैं.
ReplyDeleteThis was very helpful. Good to know the do’s and don’ts of Online Matka Play before starting.
ReplyDeleteWishing good fortune to everyone who comes across this comment! I went bankrupt last year due to failed business ideas. I used to enjoy playing the lottery for fun but as my situation worsened, I sought help to win big this time and found a man called MEDUZA, who has assisted numerous individuals worldwide with their financial issues. This man prepared a powerful spell for me and in my dreams, his spell revealed the winning lottery numbers to me just as he said. I played the game with the numbers and to my astonishment, I discovered that I had won $259 million Jackpot; I’m now free of debt. Without Meduza, I wouldn’t have made it through the tough times I experienced last year. Truly, MEDUZA is a divine presence among us. If you are currently struggling, reach out to MEDUZA through the below information's.
ReplyDeleteWhats-App: +1 807 907 2687
Email: lordmeduzatemple@hotmail.com
Face-book: lordmeduzatemple
Greetings to all, just because you had a poor outcome using spells doesn't imply that everyone will have the same experience. I want to express my sincere thanks to Lord Meduza for assisting me in winning the lottery and for aiding me in my spiritual struggles. The spell that Lord Meduza prepared for me brought me to my current position. The lottery numbers he provided resulted in a $2 million Powerball win for me. Lord Meduza has supported me in a great deal spiritually, as I was aware of the spiritual assaults from my enemies. I am grateful to him for helping me restore significant balance in my life, and at this moment, I no longer face any spiritual attacks. It took Lord Meduza two weeks to complete my work but the key point is that I received what I deserved as the lottery winner of $2 million. If you need his help, he's accessible via Email: lordmeduzatemple@hotmail.com OR WhatsApp: +1 807 907 2687 or go to his Face-book Page: Lordmeduza
ReplyDelete