In this post on Gambling and Expected Value, we look at the "NHL Lotto" lottery offered by the OLG.
Click here to find similar posts on other lotteries and games of chance.
Click here to find similar posts on other lotteries and games of chance.
NHL Lotto (OLG)
NHL Lotto a lottery offered by the Ontario Lottery and Gaming Corporation (OLG).
How the Game Works
To play NHL Lotto, the player selects a combination of 5 numbers chosen from 1 to 30, and an NHL team (of which there are also 30 options). Numbers cannot be repeated and the order is not important. The player also has the option of having the computer generate a random selection instead (known as "Quick Pick" in lottery vernacular). The game involves two portions, the "Instant Win" and the "Nightly Draw". In the Instant Win portion, you watch a computer-generated animation of a hockey player take three shots at a net with targets and hope that you've been randomly selected to be a winner. The system has been programmed to randomly mete out prizes based on OLGs predetermined odds of winning. In the Nightly Draw, prizes are awarded based on correctly matching the winning numbers and NHL team. It costs $2 to play NHL Lotto.
Probabilities and Prizes
There are 13 different ways to win a prize in the Instant Win portion of NHL Lotto, ranging from $15,000 down to $2. The prize awarded corresponds to the targets hit by your computer generated hockey player, but it's not clear how exactly that translates into calculable probabilities. I'll have to assume the odds reported by the OLG are the exact probabilities programmed into their computers. But here's the summary of the Instant Win prizes and probabilities for NHL Lotto:
There are 142,506 unique combinations of five numbers that can be chosen from the numbers 1 to 30. The number of combinations of items you can choose from a set without repetition is calculated using the following formula:
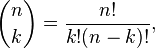
where k is the number of items chosen, n is the total number of item to choose from, and ! denotes the factorial function. In this case, n = 30 and k = 5. But you also choose one hockey team out of 30 possible choices. You could repeat the above calculation for n = 30 and k = 1, but it should be intuitively obvious that there are 30 possible ways to pick one hockey team out of the 30. So in total there are 30 times 142,506 = 4,275,180 unique combinations of one NHL team plus 5 numbers chosen from the numbers 1 to 30.
The probability of matching some number of the winning 5 can be calculated from the hypergeometric distribution. The formula looks like this:
where p is the probability of winning, n is the size of the set of numbers the winners are drawn from, k is the size of a combination, and r is the number of matching numbers required to win the prize. For example, to calculate the probability of matching four numbers in NHL Lotto, r = 4, k = 5, and n = 30. Plugging in the numbers gives the probability of approximately 0.088%, or about 1 in 1,140 (note this probability reflects the combined probability of winning either the 3rd or 4th prizes).
We can treat the NHL team matching as a bonus number drawn from a separate pool of numbers. The formula to calculate the probability of matching r out of k winning numbers plus a bonus number that is drawn from a separate pool of m numbers is a slight modification of Equation 1:
Here is a table summarizing the payouts of the Nightly Draw portion of NHL Lotto and their probabilities:
Since for some of the prizes matching x out of 5 numbers has two different prizes depending on whether or not you match the NHL team, the probability has to be adjusted for overcounting. The probability of matching with the bonus is calculated from Equation 2 (m = 30). The probability of matching without the bonus is calculated from Equation 1 minus Equation 2.
So there's roughly 66.7% chance you lose on the Instant Win game and 94.5% you lose on the Nightly Draw. The combined probability of losing both games is calculated by multiplying the two probabilities together, which works out to a 63.1% probability that an NHL Lotto player has just thrown his money away.
 |
| Summary of prizes and their probabilities in the Instant Win portion of NHL Lotto |
There are 142,506 unique combinations of five numbers that can be chosen from the numbers 1 to 30. The number of combinations of items you can choose from a set without repetition is calculated using the following formula:
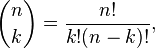
The probability of matching some number of the winning 5 can be calculated from the hypergeometric distribution. The formula looks like this:
 |
| Equation 1 (general lottery prize probability formula) |
where p is the probability of winning, n is the size of the set of numbers the winners are drawn from, k is the size of a combination, and r is the number of matching numbers required to win the prize. For example, to calculate the probability of matching four numbers in NHL Lotto, r = 4, k = 5, and n = 30. Plugging in the numbers gives the probability of approximately 0.088%, or about 1 in 1,140 (note this probability reflects the combined probability of winning either the 3rd or 4th prizes).
We can treat the NHL team matching as a bonus number drawn from a separate pool of numbers. The formula to calculate the probability of matching r out of k winning numbers plus a bonus number that is drawn from a separate pool of m numbers is a slight modification of Equation 1:
 |
| Equation 2 (general lottery with separate bonus number prize probability formula) |
Here is a table summarizing the payouts of the Nightly Draw portion of NHL Lotto and their probabilities:
 |
| Summary of prizes and their probabilities for the Nightly Draw portion of NHL Lotto. |
So there's roughly 66.7% chance you lose on the Instant Win game and 94.5% you lose on the Nightly Draw. The combined probability of losing both games is calculated by multiplying the two probabilities together, which works out to a 63.1% probability that an NHL Lotto player has just thrown his money away.
Expected Value
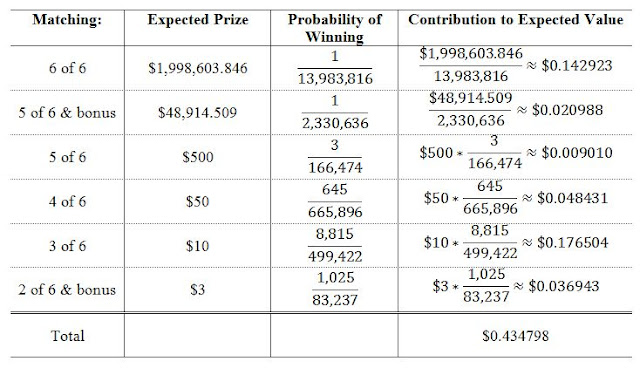
Expected value here is pretty straightforward to calculate, just multiply each of the possible prizes by its respective probability, sum all the products, and then subtract the cost of the ticket. For example, the $100,000 prize in the Nightly Draw multiplied by the 1/4,275,180 probability of winning contributes an expected value of $100,000/4,275,180 (about 2.34 cents) to the overall expected value of an NHL Lotto ticket.
From the tables, you can see there's a house edge of about 41.3%, meaning an average of 41.3 cents from every dollar spent on NHL Lotto goes straight to the OLG.
It's interesting to compare the two games. The total expected value of the Instant Win prizes is more than 4 times the expected value of Nightly Draw prizes. Similarly, the probability of getting a payout in the Instant Win portion is about 6 times the probability of getting a payout in the Nightly Draw. The OLG cleverly use a little computer animation, which is probably slightly entertaining to watch, and the fact that you get a payout about a third of the time, to hook people on the game. Most people appreciate that the chance of winning exists only if they buy a ticket, but don't really appreciate how minuscule that chance might be. The Nightly Draw is there to give players hope. The thinking is that if you lose the Instant Win game, well at least you've got another shot at free money. Too bad your chance of winning anything in the Nightly Draw is much lower than in the Instant Win. The Nightly Draw is even assigned a bigger top prize, because when the payout gets bigger, people tend to be more willing to make bad decisions (like buying another ticket).
From our analysis we can draw the following conclusions:
 |
| Summary of expected values of the prizes in the Instant Win portion of NHL Lotto |
 |
| Summary of expected values of the prizes in the Nightly Draw portion of NHL Lotto with overall expected value and house edge of NHL Lotto |
It's interesting to compare the two games. The total expected value of the Instant Win prizes is more than 4 times the expected value of Nightly Draw prizes. Similarly, the probability of getting a payout in the Instant Win portion is about 6 times the probability of getting a payout in the Nightly Draw. The OLG cleverly use a little computer animation, which is probably slightly entertaining to watch, and the fact that you get a payout about a third of the time, to hook people on the game. Most people appreciate that the chance of winning exists only if they buy a ticket, but don't really appreciate how minuscule that chance might be. The Nightly Draw is there to give players hope. The thinking is that if you lose the Instant Win game, well at least you've got another shot at free money. Too bad your chance of winning anything in the Nightly Draw is much lower than in the Instant Win. The Nightly Draw is even assigned a bigger top prize, because when the payout gets bigger, people tend to be more willing to make bad decisions (like buying another ticket).
From our analysis we can draw the following conclusions:
- NHL Lotto has a house edge of about 41.3%, which is a little better than a 50/50 draw. In other words, on average, OLG keeps 41.3 cents of every dollar spent playing NHL Lotto. Better than a lot of lotteries, but worse than casino games.
- The Instant Win portion of the game is significantly better than the Nightly Draw portion, both in terms of the expected prize value (about 4 times that of the Nightly Draw), and the odds of winning a payout (about 6 times higher chance of winning than in the Nightly Draw).
- The combination of flashy animation, small and relatively frequent payouts, and a second chance game that has a bigger top prize (but rarely pays out to anyone) is purposefully crafted to attract and hook gamblers on NHL Lotto.