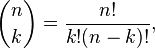In 1992, Drs. Brian Whipp and Susan Ward of the University of California published an
article in the journal
Nature claiming that women would be beating the men at the
marathon at the world elite level as early as 1998. In fact, they claimed that women will be outrunning the men in all the events by the middle of the 21st century. Needless to say, their predictions were bad. But that didn't discourage Tatem et al, a group of doctors from the University of Oxford, from publishing their own
article in
Nature in 2004. Tatem et al. essentially repeated the same analysis, and arrived at essentially the same conclusion, as Whipp and Ward. Tatem et al focused on the
100 m dash though and had a few more years worth of data to work with. However, they still concluded that women will beat men in the 100 m event at the 2156 Olympics.
 |
| Tika Gelana won the 2012 Olympic marathon in Olympic record time, but still 15 minutes behind the winner of the men's event. She would have placed 64th in the men's race. |
It's now 2014 and a woman has yet to beat all of the men at any event at any world-class track & field meet. Twenty-two years after the blunderous predictions of Whipp and Ward and women still aren't threatening to break any of the men's world records any time soon. So how exactly did these doctors arrive at such bad conclusions? They were guilty of a gross misuse of statistics. How did bad statistics get published in
Nature in 1992? I don't know. My guess is that the authors lucked out and got a peer reviewer who also knew nothing about statistics. How did essentially the same argument get published in
Nature again in 2004? I wish I knew that too. It was a "double fail" for
Nature's peer review process.
Anyway, I'm going to walk you through how to analyze world record progressions just like Tatem et al and Whipp & Ward, then provide some reasoning to demonstrate how ridiculous those authors' conclusions were.
Step 1:
Obtain the historical progression of world records from today to as far back as you can go. Whipp & Ward used records from the early 1900s up to 1992 (the
IAAF started keeping records in 1912). Tatem et al used 1912 to 2004. I'll go from as far back as I can find data for, though arguments can be made for ignoring data prior to 1912. The main one is that the IAAF hadn't yet formed and therefore older records are not ratified as world records. A weaker argument is that Excel doesn't recognize dates from before the year 1900. That problem is easily overcome though, you just have to get a little creative with how you plot the dates.
By the way, finding the data for this analysis was harder to do back when our learned doctors were drafting papers for
Nature, but today we have Wikipedia and all the world record progressions (at least the ratified records anyway) are found with ease. For example, here's the
men's 100 m record progression. I gathered my data from
here, which includes many non-ratified records. I've cross-checked some of the results to verify accuracy using this extensive
database of track results.
Step 2:
Plot the record progression on a graph in Excel. Plot either the result or the average velocity on the y-axis and the date the record was set on the x-axis. Do this for both men's and women's records. I've plotted the 100 m and marathon world record progressions below:
 |
| Normalized world record progression for the 100 m dash and marathon. |
Step 3:
Use the "Add trendline" feature in Excel to add best fit lines to the men's and women's records. Here's my plot again, but with the trendlines added:
 |
| Normalized world record progression with trendline forecasting for the 100 m dash and marathon. |
Step 4:
Extrapolate the best-fit lines and calculate the date when the men's line intersects the women's line. Boldly conclude that women will be beating men at the Olympics by the date you've calculated. I've calculated the intersections of all my trendlines and generated the table below:
 |
| Predicted dates for intersection of men's and women's world records. |
Step 5:
Write up your findings in a short article and submit it for publication in
Nature.
Here is a list of conclusions you can pretend are supported by the data:
- The 5000 m world record will be the last of the men's records to fall to the women. It probably won't happen until 2178.
- Women's records will exceed the men's records in eleven of the thirteen events by the year 2050.
- We are 20 years overdue for the intersection of the men's and women's records in sprint hurdles, based on average speed to complete the event (the sprint hurdles are 100 m for women and 110 m for men).
- We are 10 years overdue for the intersection of the men's and women's records in the 10,000 m.
- We are 8 years overdue for the intersection of the men's and women's records in the 4x400 m relay.
So, there you have it. Writing a paper for
Nature can be just that easy. But you've probably already realized that something's amiss. Let's look at a few reasons why this kind of "analysis" is completely irrational.
Reason #1: The models predict that marathon runners will eventually run faster than sprinters.
If you look at the slopes of the best-fit lines for each record progression, you'll find that most of the long distance events have steeper slopes than the sprint events. This suggests that the marathon record will eventually represent a higher average speed than the 100 m world record. I guess the marathoners will be content to use their incredible speed and super stamina only to win marathons, leaving the 100 m event to slower, less capable humans. Here are all the slopes of the lines:
 |
| Average rate of improvement in world record performances, expressed in metres per second per year. |
The women's
3000 m steeplechase record has the fastest rate of improvement, suggesting that a woman running nearly two miles and over several 30-inch high barriers will one day be the fastest human on the planet. The men's 100 m record has the lowest rate of improvement, suggesting that the men's 100 m record holders will eventually have the slowest average speed of all male and female record holders in any track event. Below are all the dates of intersection with the men's 100 m world record progression:
As you can see, in most of the events, our models predict that a woman will be outpacing the men's 100 m world record holder by the year 2100. The men running in other events will also outpace the men's 100 m world record, but it will take them, on average, 100 years longer to do it than the women.
Reason #2: A linear model to predict how fast the world's fastest human can run at a given time makes no physical sense and has no basis in reality.
Why does a linear model not make sense? Well, to start, a linear model has a zero-intercept. Meaning that the model suggests there was a time in history where the world's fastest human was stationary. If you go further back in time, the model predicts negative speeds. Speed is considered to be an absolute quantity, so negative speed has no physical meaning. A linear model also increases without bound; it suggests that there is no upper limit to how fast a human can run. Obviously, that cannot be true. The speed of light is definitely beyond reach, but a linear model suggests that we'd get there (eventually). Of course, there are more stringent restrictions related to our biology and physiology that cap human speed to far more modest levels, but we needn't get into that. The point is there are obvious limits to how fast we can run and a linear model ignores them. So here are some important and completely absurd milestones predicted for the women's 3000 m steeplechase record:
Reason #3: A model with no physical basis cannot be trusted to give meaningful results if you extrapolate beyond the data.
The average extrapolation to intersection of the trendlines was 32 years for the men and 42 years for the women. That's quite significant. The men's records often went back to the late 1800s, but the women's records rarely went back to around the 1920s. Several of the women's records only go back to around the 1970s. In the case of the 3000 m steeplechase, the records only go back to 1996 because the IAAF didn't permit women to compete at that event previously.
 |
| How far you have to extrapolate the trendlines to reach a predicted win for women over men. |
Extrapolating so far beyond your data is not a meaningful prediction. All it can tell you is what might be if the general trend you see now just happens to continue in exactly the same way long into the future.
Reason #4: In the past, female steroid users could get away with more significant performance enhancement than male steroid users.
Drug testing in the 1970s and 1980s wasn't nearly as sensitive as it is today. Steroid use was rampant and often went undetected. Several communist countries had state sponsored programs to enhance athletic performance (often without the athlete's knowledge or consent).
East Germany and the
Soviet Union were quite successful at it. This isn't to say they were the only cheaters, but they definitely had spent considerable effort researching the best way to cheat. Many
American and
Chinese athletes were
also cheating.
The reason steroid use is comparatively advantageous for females has to do with our biology. Anabolic steroids mimic the hormones that make men strong and muscular. Women have these hormones too, but in much smaller quantities (typically less than 10% of male levels). What this means is that for the same quantity of anabolic steroid, women will have a much higher increase in their relative hormone levels, and therefore experience comparatively greater enhancement of their athletic performance. I've depicted this graphically below:
 |
| Graphical comparison of an equal dose of steroids in men and women. |
What I've done is assumed that a male athlete typically has 100 units of testosterone naturally and a female athlete typically has one tenth that amount. I have then shown the effects of adding 10 units from steroids. In the male athlete, it's a 10% increase in his normal testosterone level. In the female athlete, it's a 100% increase in her normal testosterone level.
What does all this talk of steroid use mean? Well, it means that a level of steroid use too small to detect in 1980 could potentially still provide significant performance enhancement to female athletes. That might help explain why women's records are so much older than men's records: the women's records have been set almost impossibly high by the steroid-fed women of the 70s and 80s. Looking only at official Olympic running events, the average age of a men's world record is currently 8.8 years. The average age of a women's world record is more than twice that at 18.5 years.
 |
| Dates the current world records were set. |
Women simply aren't breaking records like they used to, but our prediction models don't know that.
Reason #5: Historically, fewer women have been able to train and compete in athletics. This strongly influences the slope of the best-fit line.
Many of the women's races didn't appear as Olympic events until long after the first modern Olympiad in 1896. Therefore, the men have a longer history of world-class competition in these events. Here's a list showing when each event first appeared at the Olympic games:
Furthermore, men were competing in some of these events and maintaining statistics long before the first Olympics, so the world records were well-established. Women in the past haven't pursued athletic endeavours due to various gender-biases and ill-conceived notions of female physical limitations. For instance, after six women collapsed upon completing the 800 m race at the 1928 Olympics, it became widely believed that this event was simply
too much for feminine strength. Some doctors warned that women who participated in such feats of endurance would grow old too quickly. It didn't seem to occur to everyone that these women simply hadn't trained for this event and that's why it was so hard for them. So up until around the first half of the 20th century, very few women even had the opportunity to pursue athletics and many of the women's records were just beginning to be tracked by the IAAF. Therefore, the initial women's records improved quite rapidly, since they were set by athletes who were comparatively not as well trained as male athletes at the time, in competition against a comparatively smaller pool of talent. This rapid progression early in the data set will inflate the predicted average rate of progression (i.e. increase the slope of the best-fit line). To show you what I mean, here are the women's 100 m and marathon world record progressions again, but split up to show how much faster the records were improving at the beginning.
 |
| Women's record progression in the 100 m and marathon. |
As you can see, for both events, the rate of improvement in the world record decreases in the latter half of the record progression.
To summarize, two papers prepared by medical doctors and published in
Nature suggested that women would soon outpace men in world-class athletics events. The authors (and reviewers) demonstrated poor understanding of the subject matter and did not appreciate the limitations of the analytical methods used to arrive at their conclusions. As a result, their predictions were wildly inaccurate. The moral of the story is: don't conduct an analysis that you're incompetent to perform.
And to answer the question "Will women outrun men?", the answer is "probably not". Men naturally produce more testosterone, hence are larger and stronger, ultimately making them more capable athletes. Even in the marathon, their increased size and strength gives them a bit of an edge.
References
Tatem, A. J., Guerra, C. A., Atkinson, P. M., and Hay, S. I. (2004).
Athletics: Momentous sprint at the 2156 Olympics? Nature,
431. pp. 525.
Whipp, B. J. and Ward, S. A. (1992).
Will women soon outrun men? Nature,
355. pp 25.