Gambling and Expected Value: Western 649 (WCLC)

In this post on Gambling and Expected Value, we look at the "Western 649" lottery offered by the WCLC.
Click here to find similar posts on other lotteries and games of chance.

***Note: The game conditions and prize structure of Western 649 are changing. The analysis presented here applies to Western 649 up to and including the draw taking place on October 11, 2014.*** 

Western 649 (WCLC)

Western 649 is a lottery offered by the Western Canada Lottery Corporation (WCLC). 

How the Game Works

To play Western 649, the player selects a combination of 6 numbers chosen from 1 to 49. Numbers cannot be repeated and the order is not important. The player also has the option of having the computer generate a random selection instead (known as "Quick Pick" in lottery vernacular). The six winning numbers are drawn at random, along with a seventh "bonus number". The bonus number is only important for second prize, which is awarded to tickets matching 5 out of 6 numbers plus the bonus number. Winnings are determined by how many of the numbers are matched. The minimum wager in Western 649 is $1 and additional plays are bought in $1 increments. A $1 wager buys 2 plays. 

Probabilities and Prizes

There are 5 different ways to win a prize playing Western 649, ranging from $10 to $1,000,000. The first and second prizes are capped to a total of $1,000,000 and $50,000 respectively, meaning that if there were multiple winners, the prize gets split between them.

There are 13,983,816 unique combinations of six numbers that can be chosen from the numbers 1 to 49. That number of combinations of items you can choose from a set without repetition is calculated using the following formula:

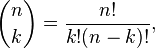
where k is the number of items chosen, n is the total number of item to choose from, and ! denotes the factorial function. In this case, n = 49 and k = 6.

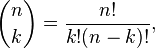
The probability of matching some number of the winning 6 can be calculated from the hypergeometric distribution. The formula looks like this:

Equation 1 (general lottery prize probability formula)

where p is the probability of winning, n is the size of the set of numbers the winners are drawn from, k is the size of a combination, and r is the number of matching numbers required to win the prize. For example, to calculate the probability of matching four numbers in Western 649, r = 4, k = 6, and n = 49. Plugging in the numbers gives the probability of approximately 0.0969%, or about 1 in 1,032.

The second prize adds a complication because of the bonus number. The formula to calculate the probability of matching r out of k winning numbers plus a bonus number (also drawn from the pool of n numbers) is a slight modification of Equation 1:

Equation 2 (general lottery with bonus number prize probability formula)

Here is a table summarizing Western 649's payouts and their probabilities:

Since matching 5 out of 6 numbers has two different prizes depending on whether or not you match the bonus, the probability has to be adjusted for overcounting. The probability of matching 6 of 6, 4 of 6, or 3 of 6 numbers is calculated from Equation 1. The probability of matching 5 of 6 plus the bonus is calculated from Equation 2. The remaining prize, matching 5 of 6 but not the bonus, is calculated from Equation 1 minus Equation 2.

The last thing we need is the probability that your wager is just money thrown away. That's 100% minus the total of probabilities of winning the prizes in the table above, which works out to exactly 245,057/249,711 (about 98.1%). This means that a Western 649 number combination has only a 1.9% chance of not losing. 

Expected Value

The precise expected value is a little tricky because the payout on the top two prizes depends on how many winners there were. Let's first start by calculating the contribution to the expected value coming from the guaranteed prize amounts. Each contribution is simply the net gain (prize minus wager) multiplied by the probability.

Next, lets calculate how much the losing tickets contribute to the expected value. Again, it's the net gain multiplied by the probability, or (-$1) * (245,057/249,711). That's about -$0.9814. At this point, the expected value of a ticket, ignoring the top two prizes, is about -$0.5321.

The last thing we have to do is figure out how much the top two prizes contribute to expected value. That depends on how many winners there are. We don't know how many winners there are, but if we know how many combinations are played, we can estimate how likely there are to be 0, 1, 2, etc. winners. This is calculated using the binomial distribution. If the probability of winning the prize is p, the probability of not winning the prize is (1-p), and N combinations are played, then probability of there being s winners of the shared pot is:

What do we need this for? Well, because the prize depends on the number of winners and the number of winners is a probabilistic function of the number of tickets sold. Therefore, we need to estimate an expected value of the prize. I've estimated that the number of combinations played in each Western 649 draw is on the order of 500,000. Accordingly, I've estimated the expected top prize based on there being up to 5 winners (more than 5 winners is too unlikely to be worth consideration). I've also checked N = 100,000 and N = 2,000,000 to show that the final result is not that sensitive to the accuracy of my estimate of N.

Probability of s winners of the top prize in a draw where N random combinations are played.
Expected prize amount estimated based on N combinations played.

The expected value of the top prize is $1,999,373.32 if 500,000 combinations are played in each draw. Remember that we're working with normalized values, so that's the prize money for a winning combination divided by the cost to play one combination. So for the top prize, the effect of prize sharing is pretty small, assuming my estimate of 500,000 combinations played per draw is reasonable. As you can see from the table, even if I was off by a factor of four and 2,000,000 combinations are played, the expected prize is still within 0.5% of the single-winner prize amount.

Working through the same process for the second prize, this time considering up to 8 winners because the likelihood of multiple second prize winners is higher, we get the following table:

Probability of s winners of the second prize in a draw where N random combinations are played.
Expected prize amount estimated based on N combinations played.

You can see from the difference between N = 500,000 and N = 2,000,000 that the expected payout for the second prize is little more sensitive to the accuracy of my estimate of N. But it is still not excessively sensitive, so our estimate is probably still pretty close to correct.

Now that we have the expected prize amounts for the top two prizes, we can finally calculate the contribution of the top two prizes to the expected value of a single combination played. Based on 500,000 combinations played per draw, the top prize contributes ($1,999,373.32 - $1) * (1/13,983,816) = $0.1430 to the expected value. The second prize contributes ($98,977.43 - $1) * (1/2,330,636) = $0.0425 to the expected value. Summing up all components, we get the expected value of -$0.3467 per $1 wagered. This means that, on average, for every dollar you spend playing Western 649, you're giving about 34.7 cents to the WCLC.

What happens if our estimate of N is wrong? Here's a table to show you:

Basically, the expected value gets worse with increased ticket sales because of prize sharing. However, as long as we're within a reasonable range of estimates of N, the expected value of Western 649 doesn't stray far from about -$0.35.


From our analysis we can draw the following conclusions:

1. A Western 649 number has less than 2% chance of winning anything.
2. Western 649's expected value is a function of the number of tickets sold, but is probably around -$0.35 per $1 wagered.
3. Based on expected value, Western 649 is actually one of the smarter purchases among different lottery tickets. The expected value is significantly better than say Pick 3 or Extra.

Addendum

In response to someone's disbelief in the accuracy of my analysis, I've verified the above results with a simple Monte Carlo simulation in this post.