 |
| A right triangle. |
A long time ago, three important trigonometric ratios were committed to memory thanks to the mnemonic SOH-CAH-TOA. These ratios are the sine, cosine, and tangent.
 |
 |
 |
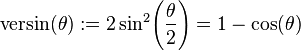 |
| The "versed sine" or "versine". |
 |
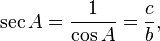 |
 |
| The reciprocal trigonometric functions. |
Which brings me to the Canadian structural concrete design standard, CSA A23.3. The folks who wrote CSA A23.3 seem to have a special place in their hearts for the cotangent. While it is certainly well within their rights to be especially fond of any mathematical function of their choosing, I don't understand why a design standard, written by engineers for engineers, would put a useless trigonometric function in a math expression. When I see a cotangent, I see unnecessary extra work. My calculator doesn't come equipped with a 'cot' button, but I do have 'sin', 'cos', and 'tan' buttons. Where there's a cotangent, I have to take a moment (however brief) to recall that the cotangent is really just the reciprocal of the tangent. I then have to rearrange the formula using the tangent in order to punch the right buttons on the calculator to get my answer.
Sure, this is only a tiny amount of extra work, even if I forget the cotangent's definition and have to do a quick internet search. But why not make the code's expression a little more practical? Save the user's time and effort by expressing formulas the way they are actually used: the way they're entered into a calculator.
Haha I love that you're doing more nerdy blogging!
ReplyDeleteThat reminded me of a similarly trigonometric rant: https://www.youtube.com/watch?v=jG7vhMMXagQ
DR EMU WHO HELP PEOPLE IN ANY TYPE OF LOTTERY NUMBERS
ReplyDeleteIt is a very hard situation when playing the lottery and never won, or keep winning low fund not up to 100 bucks, i have been a victim of such a tough life, the biggest fund i have ever won was 100 bucks, and i have been playing lottery for almost 12 years now, things suddenly change the moment i came across a secret online, a testimony of a spell caster called dr emu, who help people in any type of lottery numbers, i was not easily convinced, but i decided to give try, now i am a proud lottery winner with the help of dr emu, i won $1,000.0000.00 and i am making this known to every one out there who have been trying all day to win the lottery, believe me this is the only way to win the lottery.
Dr Emu can also help you fix this issues
(1)Ex back.
(2)Herbal cure & Spiritual healing.
(3)You want to be promoted in your office.
(4)Pregnancy spell.
(5)Win a court case.
Contact him on email Emutemple@gmail.com
What’s app +2347012841542
Website Https://emutemple.wordpress.com/
Facebook page Https://web.facebook.com/Emu-Temple-104891335203341