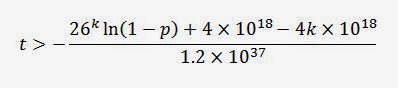Given enough time, a chimp punching keys on a typewriter at random will almost surely type out all of Shakespeare's plays.
 |
| Of course, the modern chimpanzee would choose a laptop over a typewriter for this task. |
This metaphor describes what's known as the "
infinite monkey theorem", which basically states that any finite string of characters must be contained within an infinite string of random characters. Here's the proof:
Let's start with looking at the probability of typing a particular finite string of letters on the first try. Let's also ignore all the other keys on a typewriter (or keyboard for those of you who've never seen a
typewriter) and consider just the 26 letters of the alphabet. There is a 1 in 26 chance of any particular letter being typed. We are assuming that the letters are selected randomly and independently, so the chance of typing any two particular letters is (1/26) * (1/26) = 1 in 676. Any three particular letters: (1/26)
³ = 1 in 17,576. For some number "
k" particular letters: 1 in 26 to the
k-th power. Now the probability of the inverse situation - not typing a particular letter (or block of letters) - is simply 100% minus the probability of successfully typing a particular letter (or block of letters). I've summarized in the tables below and included notes to help you understand the magnitudes of some of the numbers.
It's clear that randomly typing a short word on the first attempt is extremely unlikely. A complete sentence is practically impossible from our perspective. The chances of typing complete book at random are so exceedingly small that a physical analogy doesn't exist. Let's go off on a bit of tangent to look at some really big and really small numbers in the physical universe. The
observable universe is a sphere with a diameter of approximately 92 billion light years, or (to employ some of Mr. Spock's absurd precision) approximately 870,387,203,477,433,600,000,000,000 metres. The
Planck length represents the shortest length that, theoretically, could ever possibly be measured. It's approximately equal to 0.000 000 000 000 000 000 000 000 000 000 000 016 161 99 metre. However difficult to fathom the magnitudes of these numbers might be, just keep in mind that I can still fit them on one line in this blog post without resorting to scientific notation. The number representing the chance of successfully typing Hamlet at random on the first attempt contains 55,059 more digits than the play Hamlet does letters. Similarly, the number representing the chance of successfully typing the Bible at random on the first attempt contains 1,467,549 more digits than the Bible does letters. Here are some other really big and really small numbers to show just how small the observable universe is compared to the number of ways you can fail to type a complete work of fiction at random:
Ok, back to proving the infinite monkey theorem. We've calculated the chances of typing a string of
k letters on the first attempt. What if we had more monkeys? Let's say there are
M monkeys, each with a MacBook Air to type their random strings of letters. The probability of at least one of
M monkeys successfully typing a particular string of
k letters at random on the first attempt is:
The limit of
p as
M approaches infinity is 100%:
This means that, given enough monkeys typing randomly, the probability that at least one will successfully type a particular string of
k letters on the first attempt approaches 100%. We can also rearrange the equation above to solve for the number of monkeys necessary to ensure a given likelihood that at least one monkey will be successful on the first attempt:
I've calculated how large
M has to be to give a certain probability of success by at least one of the monkeys and summarized below.
 |
| Number of monkeys required to ensure a given probability of success on the first attempt. |
The numbers of monkeys needed to achieve a reasonable probability of success are mindbogglingly large, but they are still finite and calculable.
Ok, we've seen what happens with many monkeys, but we can look at this in a different way. What if instead of many monkeys, we have a single monkey with infinite lifespan, typing randomly and continuously. This problem is a little more interesting and the exact probability is a function of the particular pattern we're looking for. First I'll demonstrate how the probability depends on the particular pattern. Suppose you're playing "
Penney's Game" with a fair coin and want to know the chances of getting the sequence HHH or THH in a continuous sequence of tosses. The chance of getting either in the first 3 tosses is equal to 1/2 * 1/2 * 1/2 = 1/8. But as you keep going, the likelihood of THH increases because you have more potential starting points. Let's look at HHH. If you get one H, there's a 50% chance that the next toss is an H, and an equal chance it's a T. Now if you toss a second H, you have a 50% chance of completing the sequence, but if you toss a T, you have to wait at least one more toss to start over with another H. Put another way, if you're trying to get HHH but toss H and then T, you have to toss at least three more times to succeed in getting HHH. When you're after THH, if you toss a T and then another T, you're still potentially only two tosses away from success. In either case, your chance of success approaches 100% as your total number of tosses increases, but THH approaches 100% faster than HHH.


The same situation occurs with our random letters of the alphabet. The probability of finding a certain sequence of letters in a continuous random sequence depends on the sequence that you're looking for. However, the effect is less significant here because there are 26 possible outcomes per keystroke instead of just 2 and the finite string we're really after is thousands of characters long. Consider the pairs of letters AA and AS. They have equal chance of appearing in the first two letters (0.148%) of a random sequence. However, in a random three-letter sequence, AS has a 0.290% chance of appearance, compared to 0.284% for AA.
Despite the complication, there is still hope for our analysis of the monkey that ceaselessly types random letters. We can estimate a very conservative lower bound on the probability by dividing the sequence of
n letters into
n/
k non-overlapping blocks. This basically assumes that the string we're searching for must start at some multiple of
k-letters into the full sequence.
 |
| Conservative lower bound probability |
Now it'd be nice if we had an upper bound on the probability. I can't prove that this is an upper bound, and it might not necessarily always be an upper bound, but I think that it is probably likely to be an upper bound. Instead of assuming there are n/k independent trial starting points, let's assume that every letter is an independent trial starting point. Then subtract (k -1) so that we eliminate the final few letters as possible starting points (because if you start fewer than k letters from the end, you can't possibly complete the string). To give an example, if the string is PAS, you can't possibly get PAS at the end of a random letter sequence if the third-to-last letter is not 'P'. So that gives us an estimated upper limit of n - k + 1 independent trials.
 |
| Upper bound (?) probability |
The limit of both of these equations as n approaches infinity is 100%. This confirms that after typing a sufficient number of letters at random, the probability that you happened to type some finite string of letters approaches 100%.
We can also take the upper and lower bound probability and estimate the number of letters the monkey would have to type to achieve a given probability of success.
 |
| The high estimate of n, based on the low estimate of p. |
 |
| The low estimate of n, based on the high estimate of p. |
 |
| Total number of letters required in the sequence to ensure a given probability of matching a string of k letters. |
So is there any conceivable way we could actually type something like Hamlet at random? Let's forget about our metaphorical monkeys now and discuss this in terms of computing power. CPU speeds today are commonly on the order of 3 GHz. A computer with a 3 GHz CPU would not actually be able to generate random letters at a rate of 3 billion per second, but I'll be very conservative anyway to demonstrate how unlikely it is that the randomly duplicated work of fiction will ever exist. Let's assume that our computers will be able to generate random letters indefinitely at a rate of 3,000,000,000,000,000,000 (3 billion billion) letters per second. According to
this 2008 article, there were over 1 billion PCs in use at the time and there would be an estimated 2 billion in use by 2014. So let's be really conservative and assume that we employ 4,000,000,000,000,000,000 (4 billion billion) computers with the task of generating random works of literature. I'll even use the upper bound probability estimate here. How long would it take before we had a reasonable probability that at least one computer matched a particular string of
k letters at least once? Well putting it all together gives us this lovely looking equation to estimate the probability of success at any time
t (in seconds) after embarking on this endeavor:
 |
| Approximate probability of success after t seconds in our hypothetical scenario. |
Solving for
t from the approximate equation above gives us:
Which gives us an estimated lower bound time limit on matching a particular string of
k letters. The number of years it would take before we could reasonably expect a duplication of Hamlet is still mindbogglingly large (it contains 187,694 digits!). The estimated
age of the universe is only an 11 digit number of years (about 13.8 billion years). Even matching a complete sentence would take thousands of years.
Okay, let's give it one more chance. Surely the universe could duplicate Hamlet if we could enlist alien races to help out. The number of stars in the universe is estimated to be between 10 to the 22nd and 10 to the 24th powers. Let's take 100 times the high estimate and assume 10 to the 26th power. Now let's assume that 10 intelligent races exist around each star and match the computing power from our previous hypothetical scenario, and that we all coordinate to devote our total computing power to duplicating Hamlet by random letter selection. So in a grand universal waste of time, effort, and resources, we've employed {4 followed by 45 zeroes} computers spitting out random letters at a rate of 3 billion billion letters per second each. Now
p and
t are:
And we still can't duplicate Hamlet within 100 billion years with only a 1 in 1,000,000 probability. In fact, we probably can't even duplicate a short paragraph.
 |
Conservative estimate of the minimum time required to match a particular string of k letters
with given probability using the universe's combined computing power. |
So there you have it. By the Infinite Monkey Theorem, duplication of Shakespeare's work is possible with enough computing power. However, actual duplication is practically impossible from a physical perspective.
Epilogue
In 2003 the
University of Plymouth actually spent grant money (about 2,000 British pounds, equal to about $3,270 USD or $4,580 CAD at the time) to give a computer to six macaques for a month and study their "literary output". The monkeys produced only five pages of text, apparently were fond of the letter 'S', and preferred using the computer as a lavatory to doing any actual typing. Even when they were typing, they made lousy random letter generators. Some confused creationists,
such as this one, have used the results of this "study" as evidence against evolution. First, they fail to recognize that the monkeys in the "infinite monkey theorem" metaphor are meant to represent unthinking generators of random events, not actual monkeys. Actual monkeys do not act randomly. Their past experiences and their environmental conditions will influence their actions. Second, the study involved only six monkeys sharing one computer for only one month. That's hardly enough time or "monkey power" to generate a random string of letters long enough to expect anything resembling a word, let alone an entire work of fiction. Anyone who thinks this study tells us anything useful about the infinite monkey theorem is making the absurd assumption that either six monkeys is approximately equal to infinite monkeys or one month is approximately equal to infinite time.